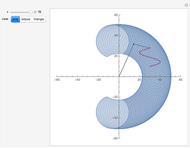
Algorithm for Bicubic Nonuniform B-Spline Surface Interpolation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
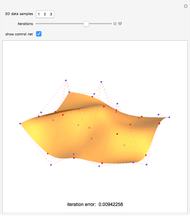
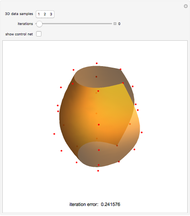
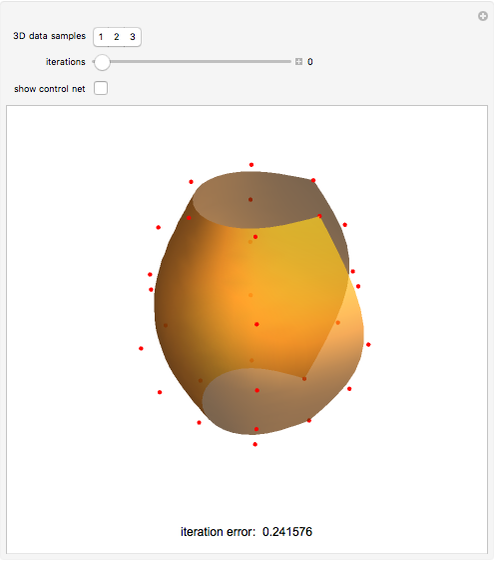
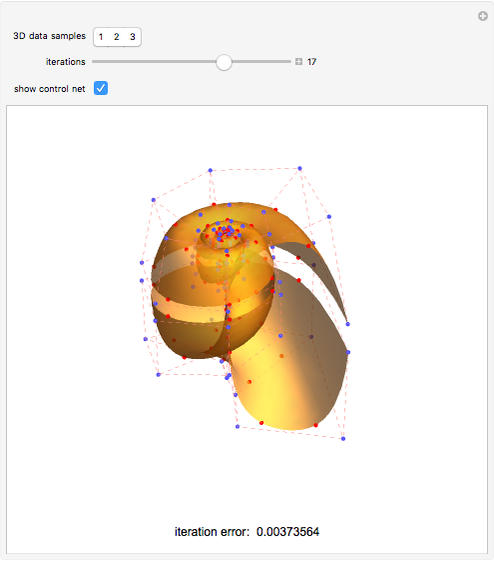
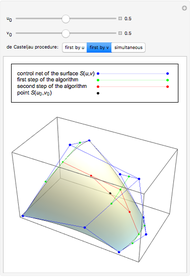
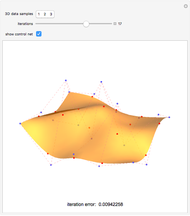
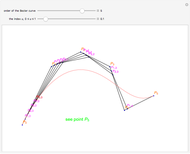
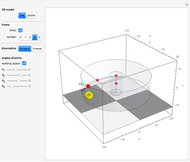
This Demonstration shows how to interpolate a set of matrix nets via a bicubic nonuniform B-spline surface and progressive-iterative approximation (PIA) technique. See Details for full implementation details.
Contributed by: Shutao Tang (December 2015)
(Northwestern Polytechnical University, Xi'an, China)
Open content licensed under CC BY-NC-SA
Snapshots
Details
We would like to use a bicubic nonuniform B-spline surface to interpolate a given set of matrix nets 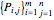 . We use the progressive-iterative approximation (PIA) algorithm rather than solving the control nets of a B-spline surface by a linear system. There are three main steps for the PIA algorithm.
. We use the progressive-iterative approximation (PIA) algorithm rather than solving the control nets of a B-spline surface by a linear system. There are three main steps for the PIA algorithm.
1. Calculating the knot vectors 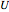 and
and  in two directions:
in two directions:

where
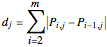
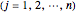 .
.
Let 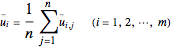 .
.
Then the knot vector 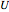 is:
is:
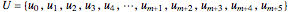 ,
,
where
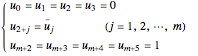
1.2 The knot vector  :
:
In a similar way, the knot vector  can be calculated.
can be calculated.
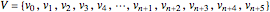 .
.
2. The iterative process:
At the start of the iteration process, let
A bicubic nonuniform B-spline surface 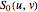 can be generated via the control nets
can be generated via the control nets 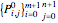 by
by
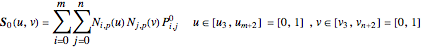 .
.
Denote the first adjustment of the  control net by
control net by
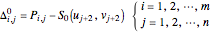
Then let
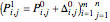
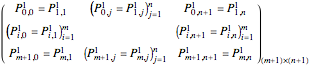
Again, a bicubic nonuniform B-spline surface  can be defined by the control nets
can be defined by the control nets  :
:
 .
.
Generally, if the 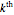 bicubic nonuniform B-spline surface
bicubic nonuniform B-spline surface 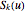 was defined by
was defined by  iterations, denoting the
iterations, denoting the  adjustment of the
adjustment of the  control net as
control net as 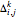 , then
, then
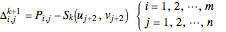
In addition, let
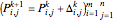
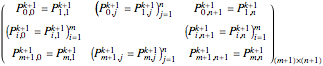
So we could generate the 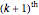 bicubic nonuniform B-spline curve
bicubic nonuniform B-spline curve 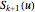 via the control nets
via the control nets 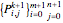 .
.
Ultimately, the surface set  can be generated, and H. Lin [1] has proved that this surface iteration format is convergent. Namely,
can be generated, and H. Lin [1] has proved that this surface iteration format is convergent. Namely,
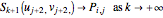
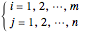
3. The error is given by
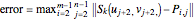 .
.
Reference
[1] 蔺宏伟, 王国瑾, 董辰世. 用迭代非均匀 B-spline 曲线(曲面)拟合给定点集[J]. 中国科学, 2003, 33(10), pp. 912–923.
H. Lin et al., "Use Iterative Non-Uniform B-Spline Curve (Surface) to Fitting Given Point Set [J]." China Science, 33(10), 2003 pp. 912–923 (in Chinese).
Permanent Citation