Global B-Spline Surface Interpolation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
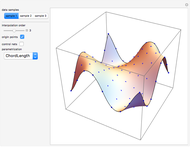
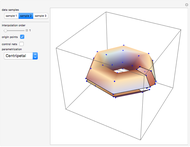
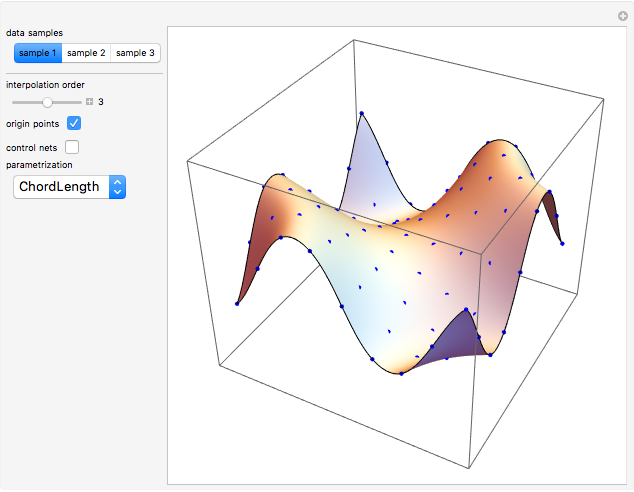
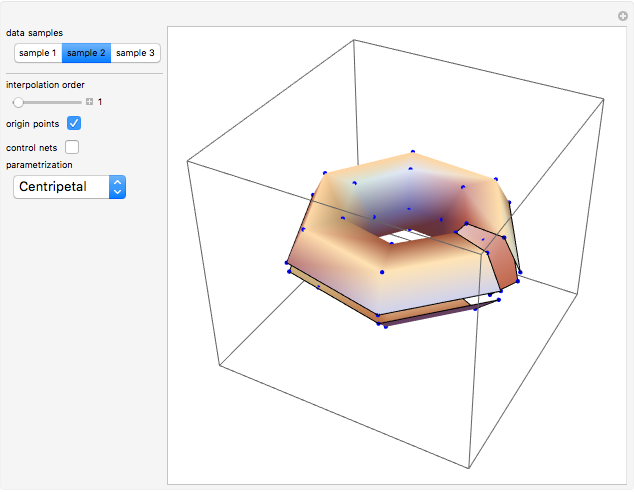
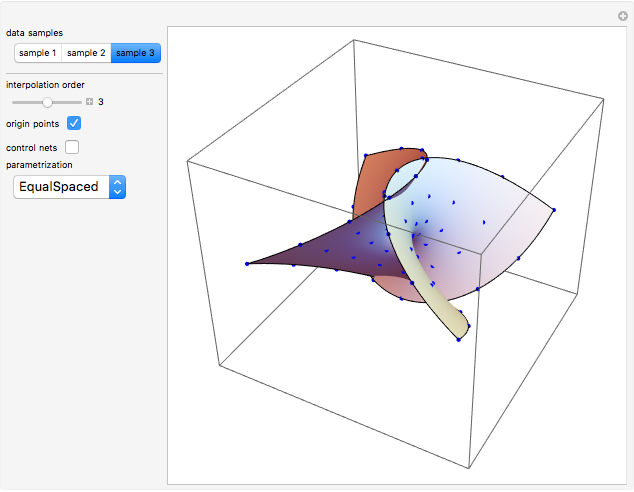
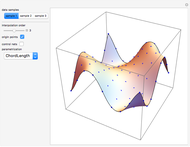
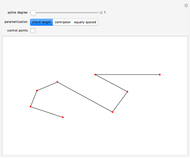
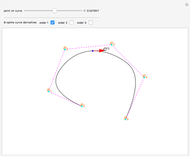
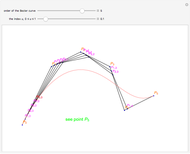
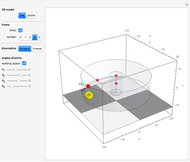
This Demonstration shows global B-spline surface interpolation. The implementation is fully described in the Details.
Contributed by: Shutao Tang (October 2015)
(Northwestern Polytechnical University, Xi'an City, China)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Given a set of 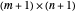 data points
data points 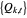 ,
, 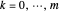 and
and 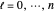 , this Demonstration constructs a nonrational
, this Demonstration constructs a nonrational  -degree B-spline surface interpolating these points, namely:
-degree B-spline surface interpolating these points, namely:
 (1)
(1)
Again, the first order of business is to compute reasonable values for the 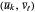 and the knot vectors
and the knot vectors 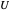 and
and 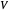 . We show how to compute the
. We show how to compute the 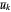 ; the
; the  are analogous.
are analogous.
A common method is to use equations (2) or (3) to compute parameters  ,
, 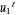 , ⋯,
, ⋯, 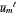 for each
for each  and then to obtain each
and then to obtain each 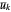 by averaging across all
by averaging across all  for
for  , that is,
, that is,
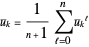 ,
, 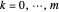 ,
,
where for each fixed  ,
, 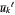 was computed by equation (2) or (3).
was computed by equation (2) or (3).
(a) Let 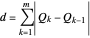 , then
, then
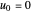 ,
, 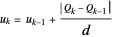 for
for 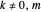 , and
, and 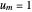 . (2)
. (2)
(b) Let  , then
, then

 for
for 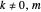 , and
, and 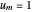 . (3)
. (3)
Once the 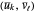 are computed, the knot vectors
are computed, the knot vectors 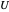 and
and  can be obtained by equation (4):
can be obtained by equation (4):
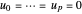 ,
, 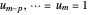 ,
, 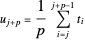 ,
, 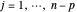 . (4)
. (4)
Now to the computation of the control points. Clearly, equation (1) represents  linear equations in the unknown
linear equations in the unknown 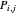 . However, since
. However, since 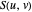 is a tensor product surface, the
is a tensor product surface, the  can be obtained more simply and efficiently as a sequence of curve interpolations.
can be obtained more simply and efficiently as a sequence of curve interpolations.
For fixed  , write equation (1) as
, write equation (1) as
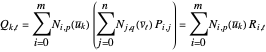 , (5)
, (5)
where  . (6)
. (6)
Notice that equation (5) is just curve interpolation through the points 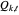 . The
. The 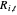 are the control points of the isoparametric curve on
are the control points of the isoparametric curve on 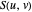 at fixed
at fixed 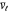 . Now fixing
. Now fixing  and letting
and letting  vary, equation (6) is curve interpolation through the points
vary, equation (6) is curve interpolation through the points 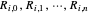 , with
, with 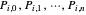 as the computed control points. Thus, the algorithm to obtain all the
as the computed control points. Thus, the algorithm to obtain all the 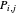 is as follows:
is as follows:
1. Using 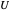 and the
and the 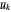 , do
, do 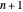 curve interpolations through
curve interpolations through  , which yields the
, which yields the 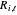 .
.
2. Using  and the
and the 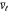 , do
, do 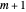 curve interpolations through
curve interpolations through 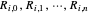 , which yields the
, which yields the 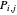 .
.
Reference
[1] L. Piegl and W. Tiller, The NURBS Book, 2nd ed., Berlin: Springer-Verlag, 1997 pp. 376–382.
Permanent Citation