Structural Instability of a Supercritical Pitchfork Bifurcation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
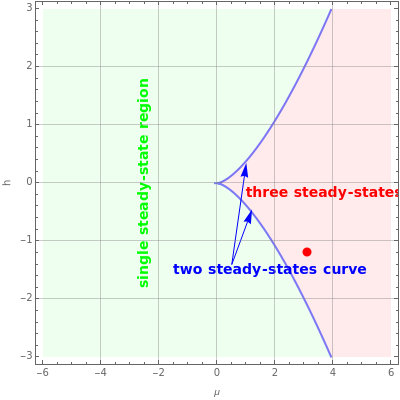
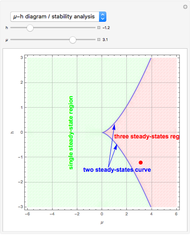
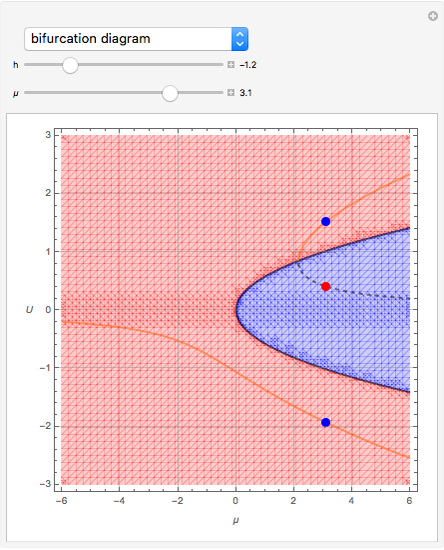
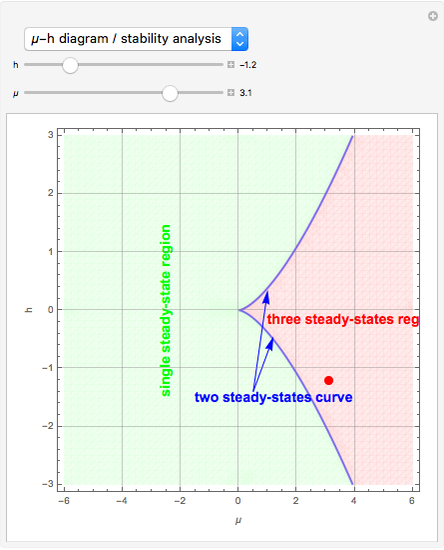
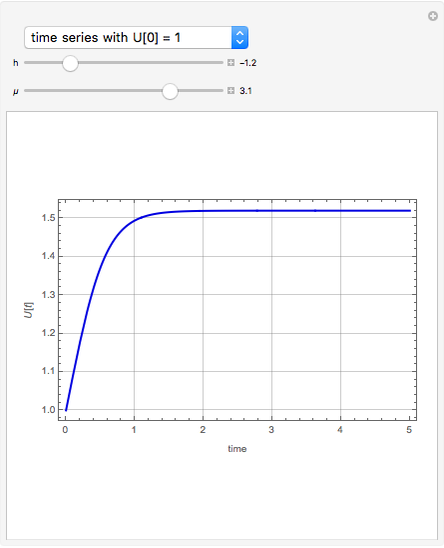
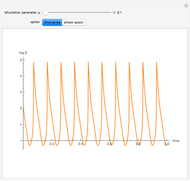
A dynamical system is structurally unstable when small perturbations alter the qualitative behavior of trajectories. An example of structural instability is the flow pattern that can occur in a two-dimensional flow field subjected to a sudden expansion [1]. In that case the stability analysis can be reduced to studying the following generic amplitude  equation:
equation:  . The steady-state amplitudes of the perturbation are the real solutions of the following nonlinear equation:
. The steady-state amplitudes of the perturbation are the real solutions of the following nonlinear equation:  . Here,
. Here,  is called the imperfection parameter. When
is called the imperfection parameter. When  , the dynamical system exhibits the classical supercritical pitchfork bifurcation.
, the dynamical system exhibits the classical supercritical pitchfork bifurcation.
Contributed by: Brian G. Higgins and Housam Binous (June 2011)
Open content licensed under CC BY-NC-SA
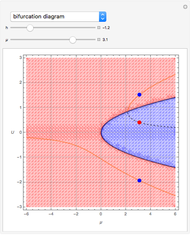
Snapshots
Details
References
[1] J. Mizushima and Y. Shiotani, "Structural Instability of the Bifurcation Diagram for Two-Dimensional Flow in a Channel with a Sudden Expansion," Journal of Fluid Mechanics, 420, 2000 pp. 131–145.
[2] P. G. Drazin and W. H. Reid, Hydrodynamic Stability, Cambridge: Cambridge University Press, 1981.
Permanent Citation