Crystal Field Theory for Coordination Complexes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
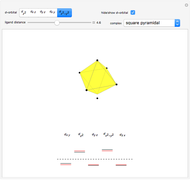
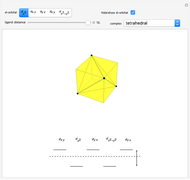
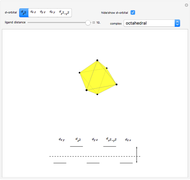
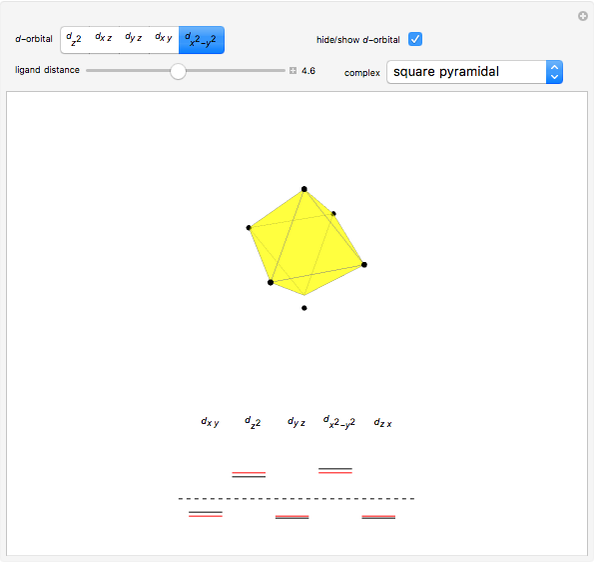
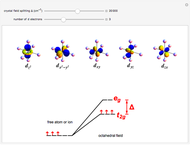
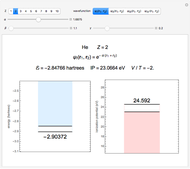
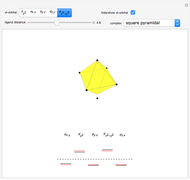
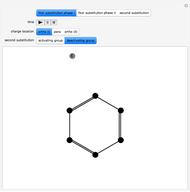
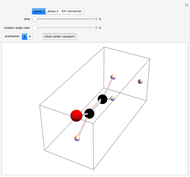
This Demonstration introduces crystal-field theory, which describes the geometry and energetics of coordination complexes. According to this model, ligands bonded to transition metal cause splitting of the  -orbitals by electrostatic repulsion between the electrons in the
-orbitals by electrostatic repulsion between the electrons in the  -orbitals and the negatively charged ligands.
-orbitals and the negatively charged ligands.
Contributed by: D. Meliga and S. Z. Lavagnino (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
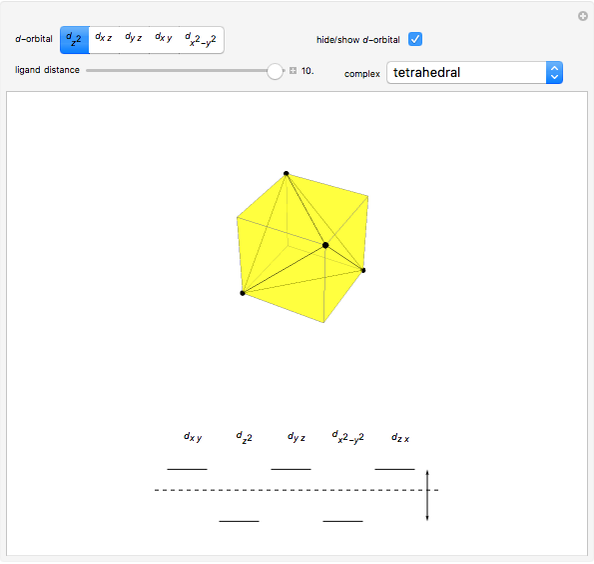
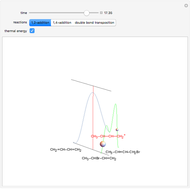
Snapshot 1: the splitting caused by the tetragonal field is shown; three orbitals increase their energy, while two decrease it
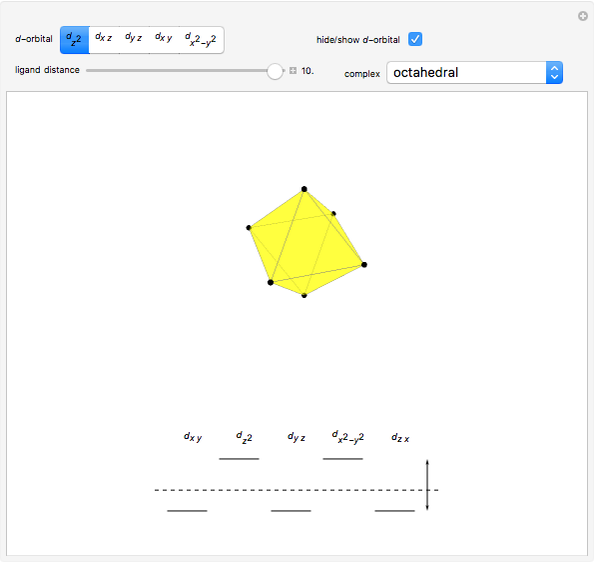
Snapshot 2: the splitting caused by the octagonal field is shown; three orbitals decrease their energy, while two increase it
Snapshot 3: planar complex derived from the octagonal field; starting levels are represented in red, while the final situation is black
Reference
[1] C. E. Housecroft and A. G. Sharpe, Inorganic Chemistry, 3rd ed., London: Pearson Education, Ltd., 2008.
Permanent Citation