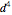d-Orbitals in an Octahedral Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
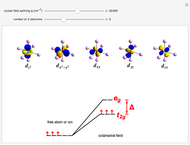
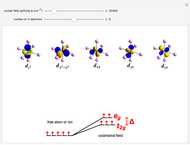
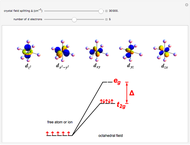
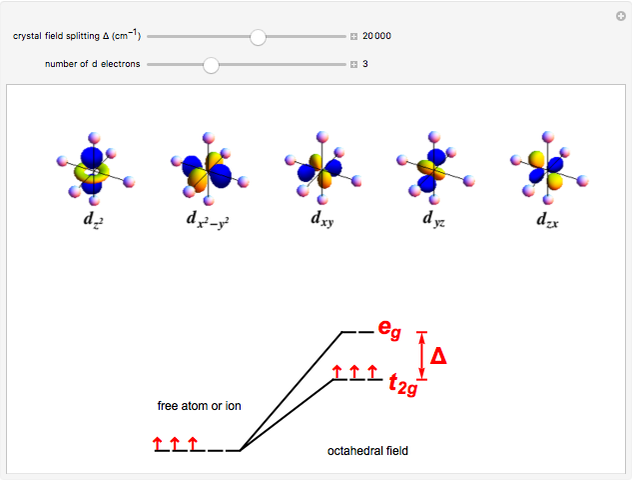
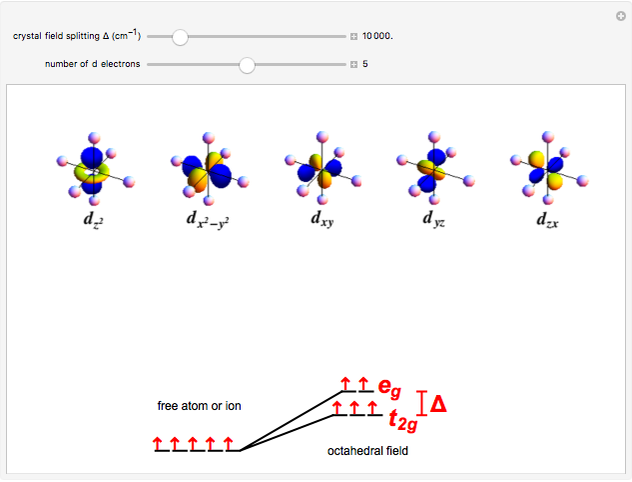
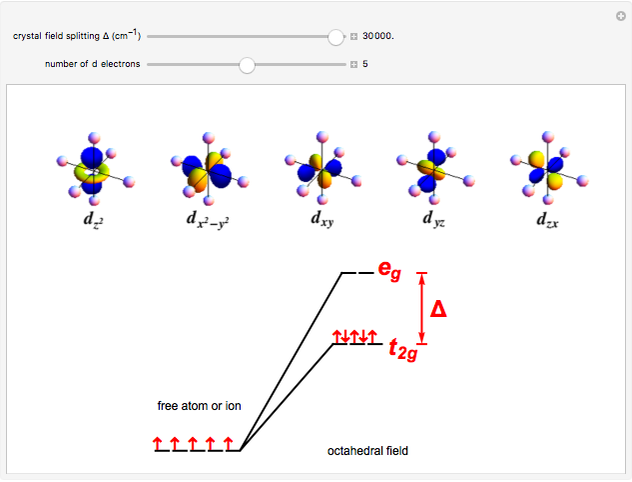
A free transition-metal atom or ion has five-fold degenerate  -orbitals, pictured at the top of the graphic. These can be occupied by a maximum of 10 electrons. The positive and negative regions of the wavefunctions are shown in the blue and yellow spheres, respectively. Transition metals are likely to form compounds in which they are centrally bonded to several molecules or ions, known as ligands. These are shown as white spheres. A common configuration is the highly symmetrical octahedral complex, in which six equivalent ligands are bound to the central ion. The effect of the ligands can be represented by a crystal field parameter
-orbitals, pictured at the top of the graphic. These can be occupied by a maximum of 10 electrons. The positive and negative regions of the wavefunctions are shown in the blue and yellow spheres, respectively. Transition metals are likely to form compounds in which they are centrally bonded to several molecules or ions, known as ligands. These are shown as white spheres. A common configuration is the highly symmetrical octahedral complex, in which six equivalent ligands are bound to the central ion. The effect of the ligands can be represented by a crystal field parameter  , whose magnitude is typically in the range 7,000–30,000
, whose magnitude is typically in the range 7,000–30,000  . The octahedral crystal field partially breaks the five-fold symmetry of the
. The octahedral crystal field partially breaks the five-fold symmetry of the  -orbitals. The
-orbitals. The  and
and  orbitals, which have lobes directed at ligands, become a higher-energy doublet which transforms as the
orbitals, which have lobes directed at ligands, become a higher-energy doublet which transforms as the  representation of the octahedral group. The remaining
representation of the octahedral group. The remaining  -orbitals transform as a triply degenerate
-orbitals transform as a triply degenerate  representation.
representation.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1:  ion in an octahedral field
ion in an octahedral field
Snapshot 2: "high-spin"  ion in a weak crystal field, for example
ion in a weak crystal field, for example 
Snapshot 3: "low-spin"  ion in a strong crystal field, for example
ion in a strong crystal field, for example 
Reference: S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Academic Press, 2004 pp. 149–153.
Permanent Citation