Death Penalty Regressions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
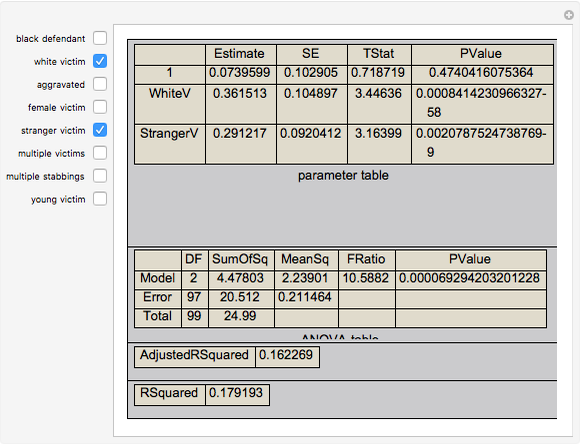
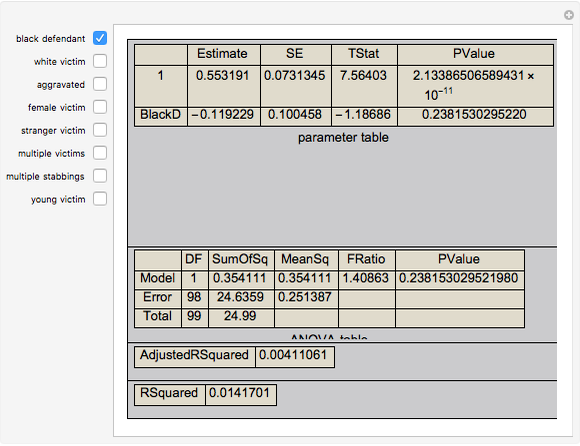
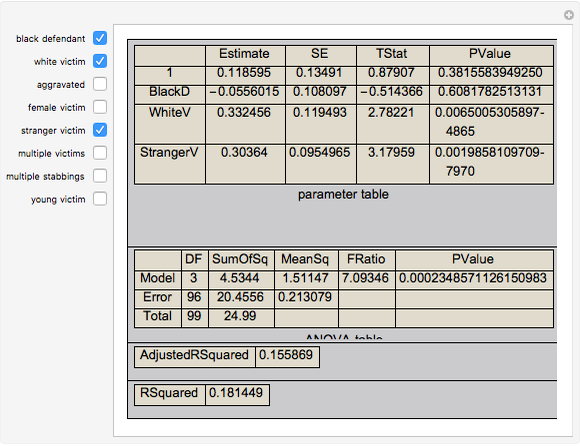
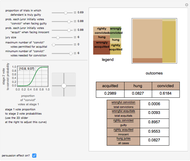
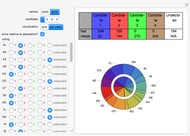
This Demonstration permits exploration of a famous dataset collected by Professor David Baldus involving the results of 100 Georgia criminal cases from arrests between March 1973 and June 1983 in which the death penalty was a potential punishment and there were eight explanatory variables. Defendants were arrested in Georgia between March 1973 and June 1983, convicted after trial of murder, and sentenced to life imprisonment or death. You may select the variables to be included in a multiple regression and see the power of those variables to explain any sentencing patterns.
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The independent variables are:
black defendant — whether the defendant was "black"
white victim — whether the victim was "white"
aggravated — whether various aggravating factors were present
female victim — whether the victim was female
stranger victim — whether the victim was a stranger to the defendant
multiple victims — whether there were multiple victims of the crime
multiple stabbings — whether there were multiple stab wounds involved
young victim — whether the victim was a minor
Technically, one should probably be using nonlinear regression techniques such as logit or probit regression to analyze this data, in which the dependent variable can only take on values 0 or 1. Linear regression is used here for the sake of simplicity.
The data used in this Demonstration is available online in Excel format at http://www.publicpolicy.umd.edu/puaf610/notes/10-Multiple_regression/death-penalty.xls. The analysis of a superset of this data did not persuade the United States Supreme Court, in McCleskey v. Kemp, 481 U.S. 279 (1987), that the death penalty violated the United States Constitution.
Permanent Citation
"Death Penalty Regressions"
http://demonstrations.wolfram.com/DeathPenaltyRegressions/
Wolfram Demonstrations Project
Published: March 7 2011