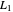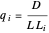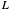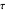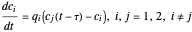Diffusion through a Membrane

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
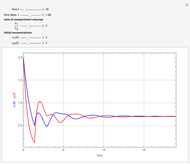
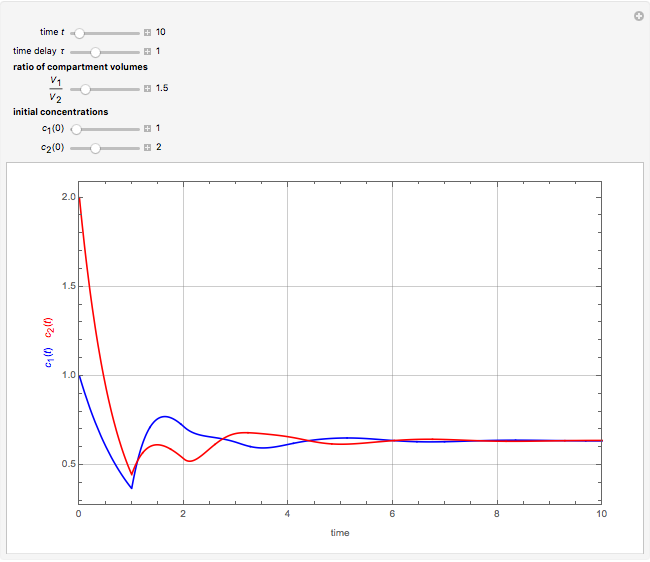
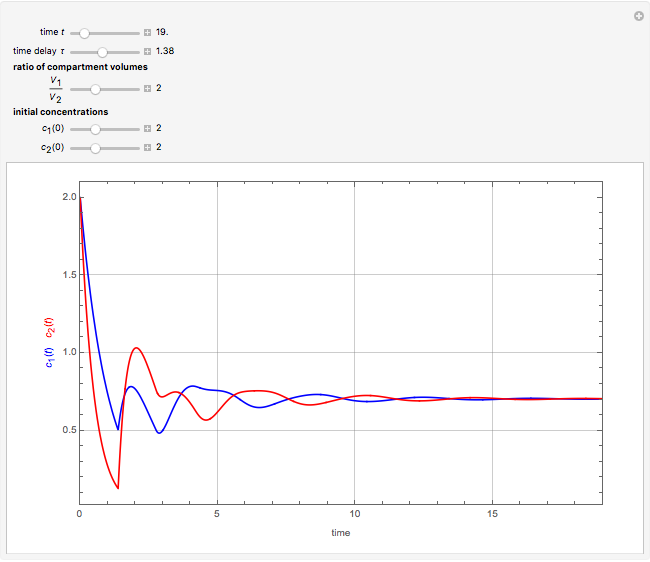
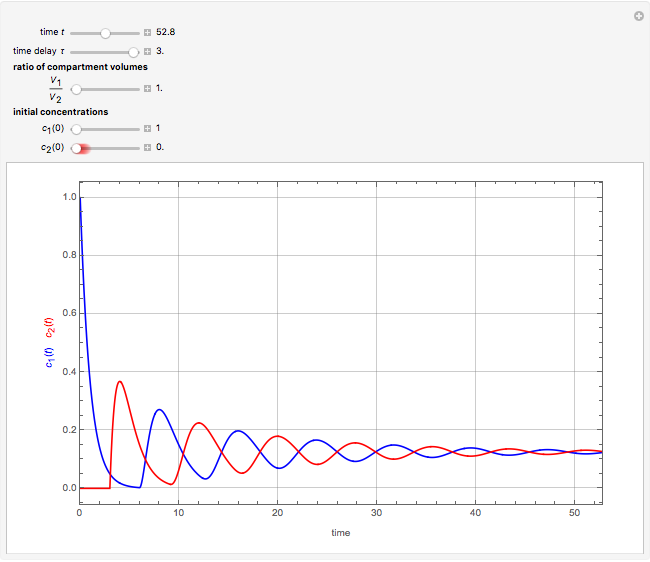
This Demonstration shows the effect of time delay on the dynamics of a simple diffusion model.
[more]
Contributed by: Clay Gruesbeck (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
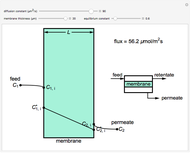
What is the meaning of the highly counterintuitive and apparently nonphysical behavior? The key lies in the fact that the final equilibrium value of  lies significantly below the starting concentrations in the two compartments. The oscillations occur while the initially empty membrane is filling up. Consider the case of equal initial concentrations with cell
lies significantly below the starting concentrations in the two compartments. The oscillations occur while the initially empty membrane is filling up. Consider the case of equal initial concentrations with cell  much longer than cell
much longer than cell  . In the first interval
. In the first interval  , the same number of molecules leaves each cell, but, because cell
, the same number of molecules leaves each cell, but, because cell  is smaller, its concentration drops further. At time
is smaller, its concentration drops further. At time  , when molecules begin to arrive, the effect is reversed, and the concentration in cell
, when molecules begin to arrive, the effect is reversed, and the concentration in cell  rises more rapidly than that in cell
rises more rapidly than that in cell  . Since molecules are now flowing in both directions, the effect will soon damp out. Readers may find the above result more convincing if they try to picture how the initially equal densities of people in two rooms of very different sizes connected by identical doors through an anteroom will change in time if, when the doors are opened, people move from room to room with equal probability and equal velocity without collisions. It is also reassuring to observe that when the results are averaged over a realistic distribution of
. Since molecules are now flowing in both directions, the effect will soon damp out. Readers may find the above result more convincing if they try to picture how the initially equal densities of people in two rooms of very different sizes connected by identical doors through an anteroom will change in time if, when the doors are opened, people move from room to room with equal probability and equal velocity without collisions. It is also reassuring to observe that when the results are averaged over a realistic distribution of  (which results, among other things, from molecular collisions within the membrane), the oscillations disappear and the concentrations behave monotonically as expected.
(which results, among other things, from molecular collisions within the membrane), the oscillations disappear and the concentrations behave monotonically as expected.
Reference
[1] I. R. Epstein, "Delay Effects and Differential Delay Equations in Chemical Kinetics," International Reviews in Physical Chemistry, 11(1), 1992 pp. 135–160.
Permanent Citation