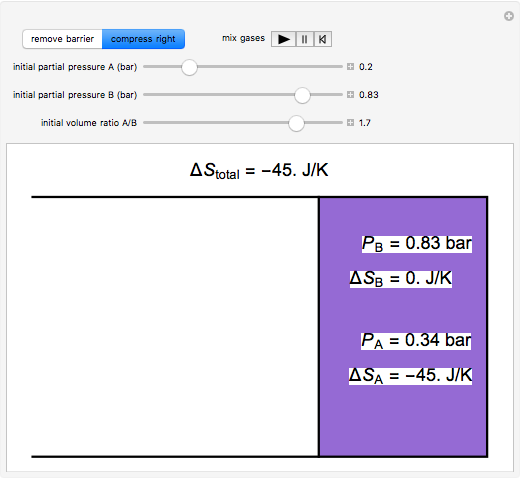
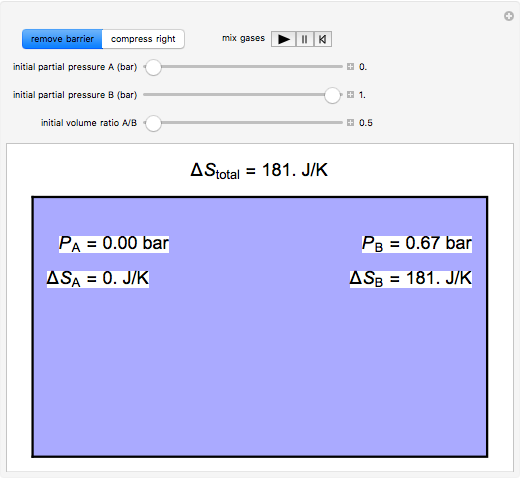
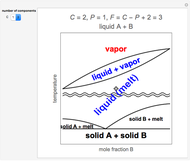
Entropy Changes in Mixing Ideal Gases

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
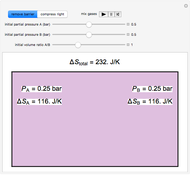
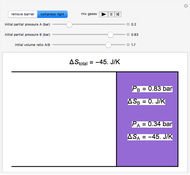
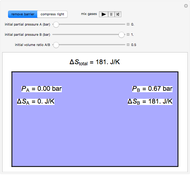
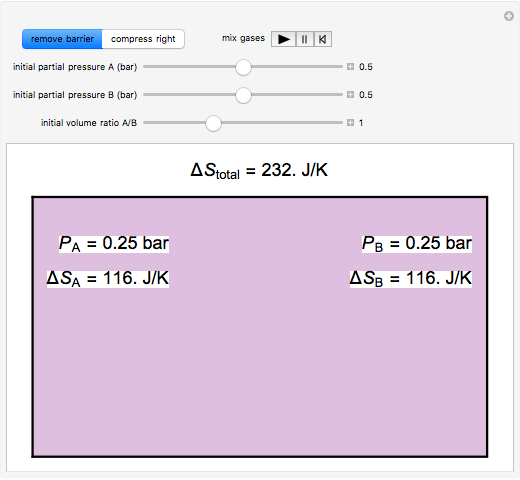
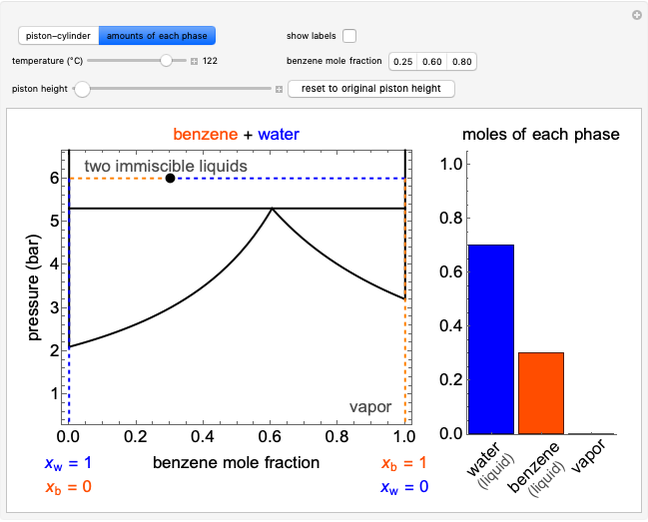
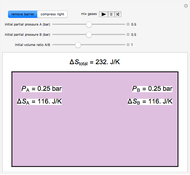
In this Demonstration, ideal gases  and
and  are mixed isothermally by keeping the total volume constant (remove barrier option) or by adding gas
are mixed isothermally by keeping the total volume constant (remove barrier option) or by adding gas  to gas
to gas  so the final volume is the same as the initial volume of
so the final volume is the same as the initial volume of  (select "compress right"). Click the play button next to "mix gases" to initiate mixing. For "remove barrier", the entropy change of each gas is the same as that of a gas expanding into a vacuum. When the partial pressure decreases, entropy increases. For "compress right", if the partial pressure of a gas does not change, its entropy does not change, even when mixed with another gas. The total entropy change is the sum of the entropy changes of each gas. Gas
(select "compress right"). Click the play button next to "mix gases" to initiate mixing. For "remove barrier", the entropy change of each gas is the same as that of a gas expanding into a vacuum. When the partial pressure decreases, entropy increases. For "compress right", if the partial pressure of a gas does not change, its entropy does not change, even when mixed with another gas. The total entropy change is the sum of the entropy changes of each gas. Gas  is colored red and gas
is colored red and gas  is colored blue, and when the gases mix, different shades of purple result, depending on the ratio of moles of each species. As the pressures increase, the color becomes more intense. When the initial pressures of
is colored blue, and when the gases mix, different shades of purple result, depending on the ratio of moles of each species. As the pressures increase, the color becomes more intense. When the initial pressures of  and
and  are equal and the "remove barrier" is selected, which corresponds to mixing at constant pressure, the entropy of mixing is
are equal and the "remove barrier" is selected, which corresponds to mixing at constant pressure, the entropy of mixing is  , where
, where  and
and  are the mole fractions of
are the mole fractions of  and
and  in the final mixture.
in the final mixture.
Contributed by: Derek M. Machalek (June 2015)
Additional contributions by: John L. Falconer and Rachael L. Baumann
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The total volume of the container is 2 
 ,
,
 ,
,
 ,
,
or
 ,
,
 ,
,
where  represents the number of moles,
represents the number of moles,  is the gas constant (J/[K mo]),
is the gas constant (J/[K mo]),  is the entropy change (J/K),
is the entropy change (J/K),  is the pressure (bar),
is the pressure (bar),  is the volume (
is the volume ( ), the subscripts
), the subscripts  and
and  represent the gases used, and the subscripts
represent the gases used, and the subscripts  and
and  represent the final and initial pressures.
represent the final and initial pressures.
The screencast video at [1] explains how to use this Demonstration.
Reference
[1] Entropy Changes in Mixing Ideal Gases. www.colorado.edu/learncheme/thermodynamics/EntropyChangesMixingIdealGases.xhtml.
Permanent Citation