Fourier Series Coefficients of a Rectangular Pulse Signal

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
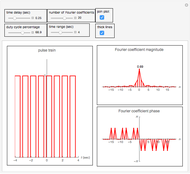
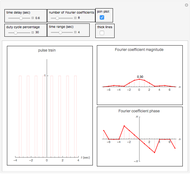
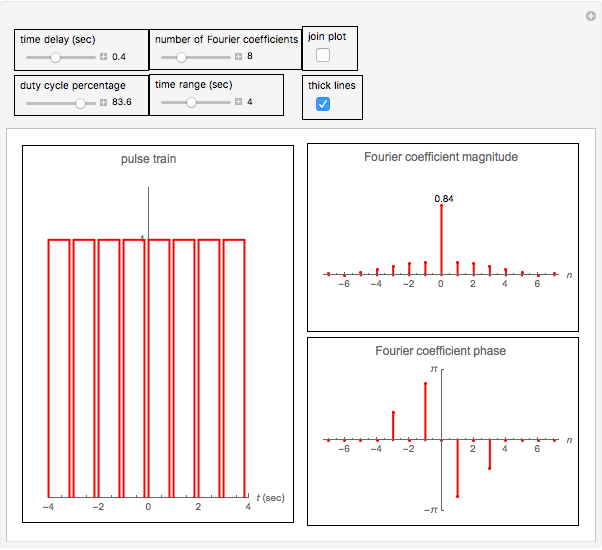
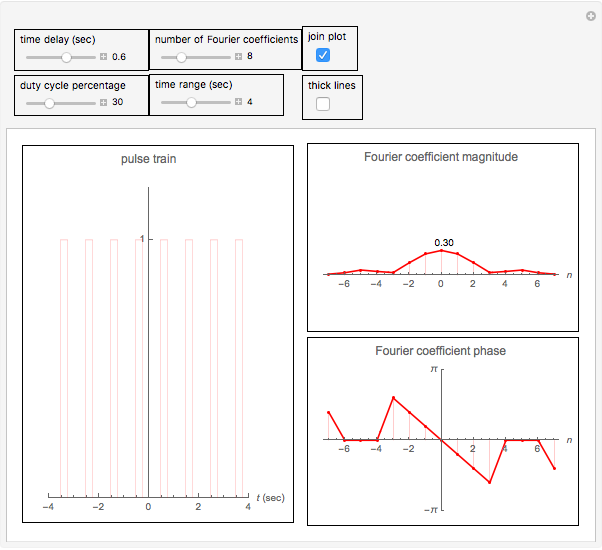
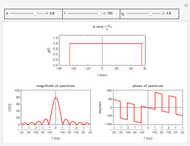
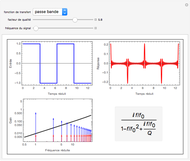
This Demonstration determines the magnitude and phase of the Fourier coefficients for a rectangular pulse train signal. A rectangular pulse is defined by its duty cycle (the ratio of the width of the rectangle to its period) and by the delay of the pulse. In this Demonstration, the pulse period is fixed at one second and the height is fixed at unity. You can vary the delay and the duty cycle as well as the number of Fourier coefficients. Since the signal is a real signal, the magnitude plot is an even function and the phase plot is an odd function.
Contributed by: Nasser M. Abbasi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The  Fourier coefficient of a rectangular pulse train is given by
Fourier coefficient of a rectangular pulse train is given by  , where
, where  is the pulse height,
is the pulse height,  is the duty cycle,
is the duty cycle,  is the period of the pulse train,
is the period of the pulse train,  is the delay of the pulse in seconds, and
is the delay of the pulse in seconds, and  . This Demonstration displays the magnitude and phase of
. This Demonstration displays the magnitude and phase of  .
.
Permanent Citation
"Fourier Series Coefficients of a Rectangular Pulse Signal"
http://demonstrations.wolfram.com/FourierSeriesCoefficientsOfARectangularPulseSignal/
Wolfram Demonstrations Project
Published: March 7 2011