Gershgorin Circle Theorem

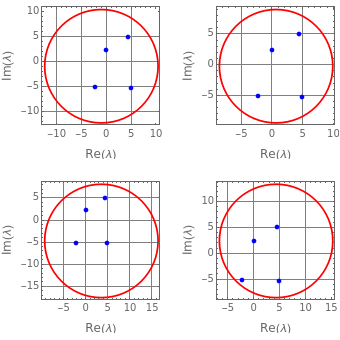
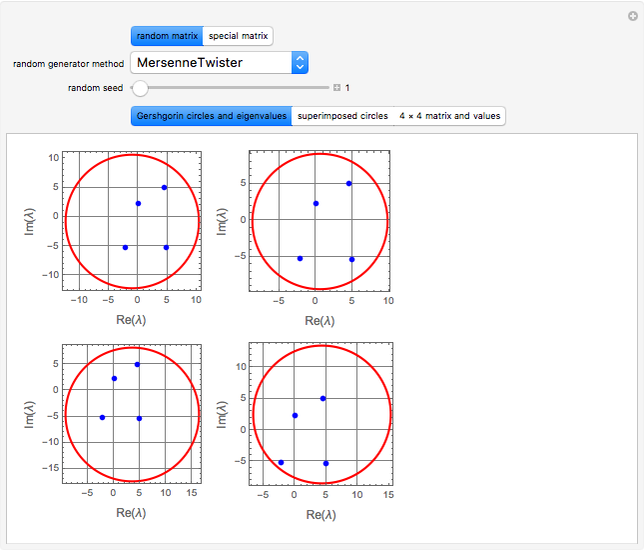
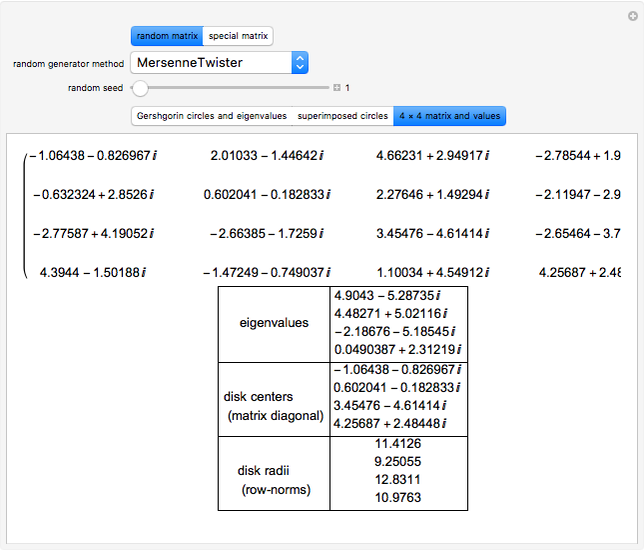
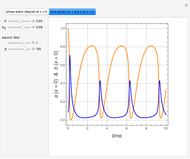
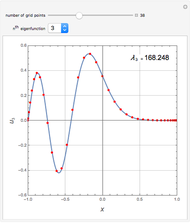
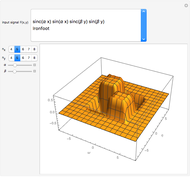
This Demonstration illustrates how the Gershgorin circle theorem can be used to bound the eigenvalues of an matrix . The theorem states that the eigenvalues of must lie in circles defined in the complex plane that are centered on the diagonal elements of with radii determined by the row-norms of , that is, and . If of the circles form a connected region disjoint from the remaining 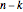circles, then the region contains exactly eigenvalues.

You can select a random matrix or a special matrix that has at least one disjoint Gershgorin circle. The elements of the random matrix, as well as some elements of the special matrix, can be changed by selecting a pseudorandom number generator from the dropdown menu. You can see either the separate Gershgorin circles with the eigenvalues or a plot that superimposes all the circles.