Heterogeneous Chemical Equilibrium with Calcium Carbonate

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
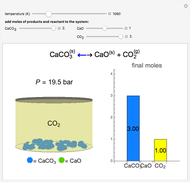
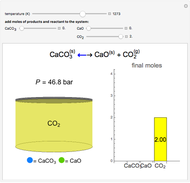
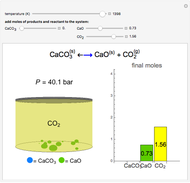
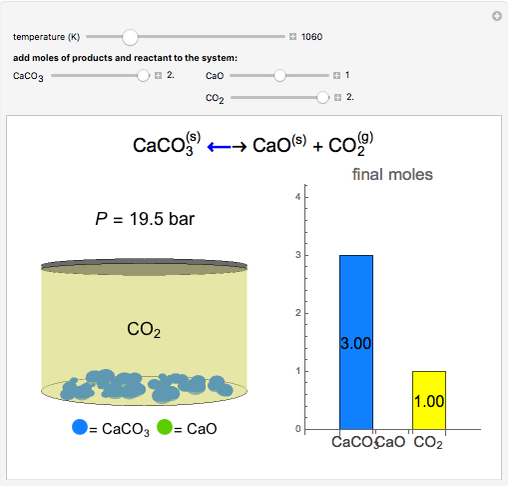
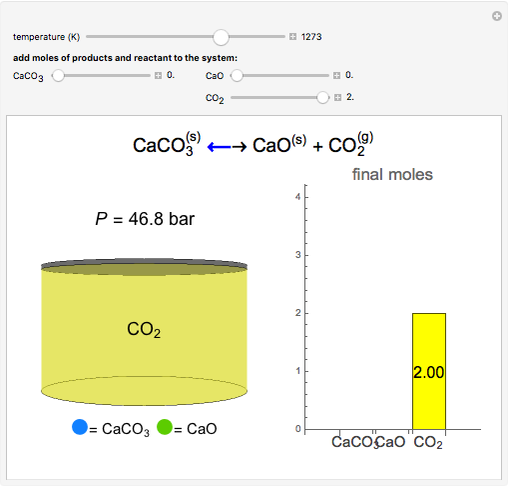
Solid calcium carbonate (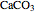 ) decomposes into solid calcium oxide (
) decomposes into solid calcium oxide ( ) and gaseous carbon dioxide (
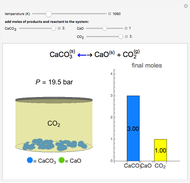
) and gaseous carbon dioxide (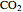 ) in a constant-volume container at high temperatures. Carbon dioxide is assumed to be an ideal gas, and the two solids are assumed to be in separate phases. You can vary the number of moles of
) in a constant-volume container at high temperatures. Carbon dioxide is assumed to be an ideal gas, and the two solids are assumed to be in separate phases. You can vary the number of moles of 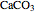 ,
,  , and
, and 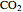 added to the constant-volume container using sliders. The container displays the equilibrium pressure; the color intensity of the gas phase increases as the number of moles of
added to the constant-volume container using sliders. The container displays the equilibrium pressure; the color intensity of the gas phase increases as the number of moles of 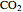 increases. The bar graph on the right shows the number of moles present at equilibrium. The equilibrium constant
increases. The bar graph on the right shows the number of moles present at equilibrium. The equilibrium constant 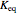 changes as the temperature changes using the slider. The equilibrium constant is equal to the
changes as the temperature changes using the slider. The equilibrium constant is equal to the 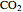 pressure (in bar) divided by the standard-state pressure of 1 bar. Note that adding more
pressure (in bar) divided by the standard-state pressure of 1 bar. Note that adding more  when
when  is already in the container (or adding more
is already in the container (or adding more 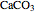 when
when 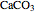 is already in the container) at equilibrium does not change equilibrium because increasing the number of moles of a pure solid does not change its fugacity.
is already in the container) at equilibrium does not change equilibrium because increasing the number of moles of a pure solid does not change its fugacity.
Contributed by: Rachael L. Baumann and Garrison Vigil (February 2015)
Additional contributions by: John L. Falconer and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For this reaction, the equilibrium constant is equal to the equilibrium pressure (in bar) divided by 1 bar pressure. The equilibrium constant is calculated as a function of temperature using the Van't Hoff equation:
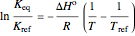 ,
,
 ,
,
where the subscript 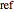 refers to a reference state,
refers to a reference state, 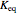 is the equilibrium constant,
is the equilibrium constant, 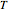 is temperature (K),
is temperature (K), 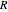 is the ideal gas constant,
is the ideal gas constant, 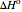 is the standard enthalpy of reaction (kJ/mol), and
is the standard enthalpy of reaction (kJ/mol), and 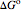 is the standard Gibbs free energy of reaction (kJ/mol).
is the standard Gibbs free energy of reaction (kJ/mol).
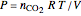 ,
,
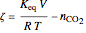 ,
,
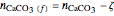 ,
,
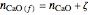 ,
,
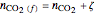 ,
,
where 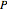 is the pressure (bar),
is the pressure (bar), 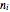 is the number of moles of component
is the number of moles of component 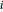 initially in the system,
initially in the system, 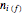 is the final number of moles in the system,
is the final number of moles in the system,  is the fixed volume of the container (
is the fixed volume of the container (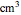 ), and
), and 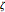 is the extent of reaction.
is the extent of reaction.
The screencast video at [1] explains how to use this Demonstration.
Reference
[1] Heterogeneous Chemical Equilibrium with Calcium Carbonate. www.colorado.edu/learncheme/thermodynamics/HeterogeneousChemicalEquilibriumCaCO3.html.
Permanent Citation