Mass Balances for Binary Vapor-Liquid Equilibrium (VLE)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
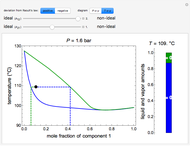
This Demonstration illustrates what happens to a binary mixture, initially in vapor-liquid equilibrium, when a pure component is added at constant temperature and pressure. If both phases remain after the addition, it illustrates how the phase mole fractions remain constant (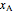 is the mole fraction of
is the mole fraction of  in the liquid,
in the liquid, 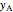 is the mole fraction of
is the mole fraction of  in the vapor). If enough of either pure component is added, the mixture is transformed to a single phase. The initial vapor-liquid mixture contains 2 mol of
in the vapor). If enough of either pure component is added, the mixture is transformed to a single phase. The initial vapor-liquid mixture contains 2 mol of  and 2 mol of
and 2 mol of  at a pressure of 3 bar. Select the button "add
at a pressure of 3 bar. Select the button "add  " or "add
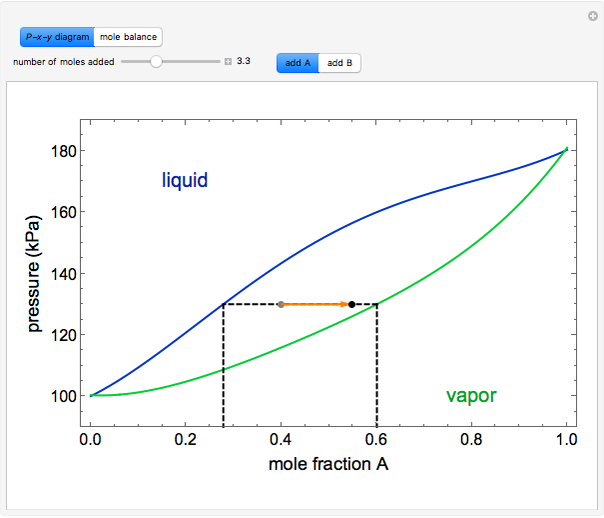
" or "add  " and use the slider to set the amount added. Adding a pure component changes the overall mole fraction of
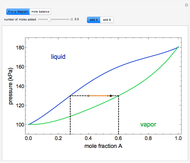
" and use the slider to set the amount added. Adding a pure component changes the overall mole fraction of  in the mixture, as represented by the black point on the
in the mixture, as represented by the black point on the 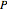 -
- -
- diagram. If the overall mole fraction of
diagram. If the overall mole fraction of  stays within the phase envelope, then
stays within the phase envelope, then 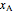 and
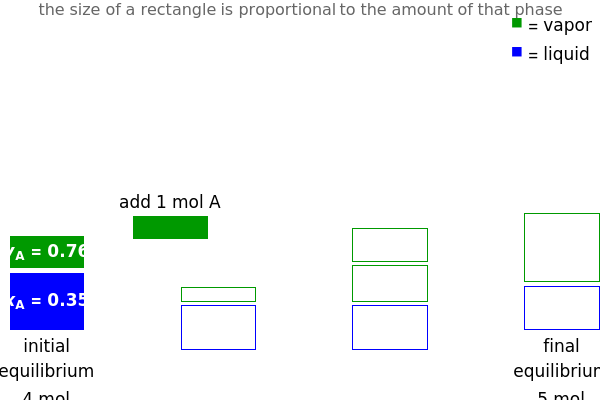
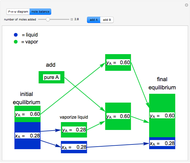
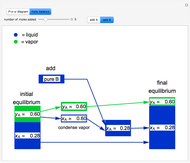
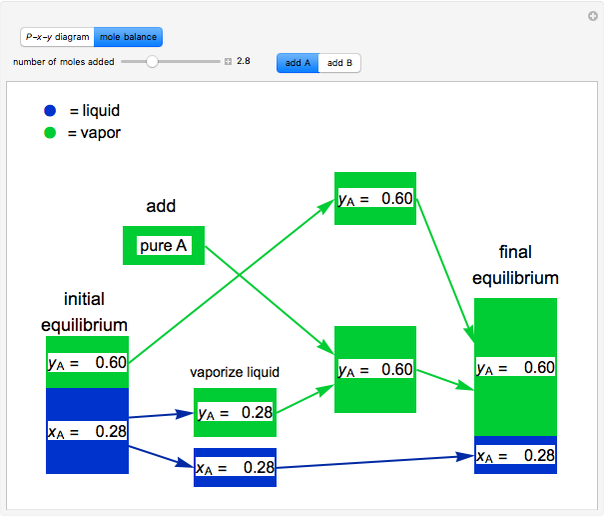
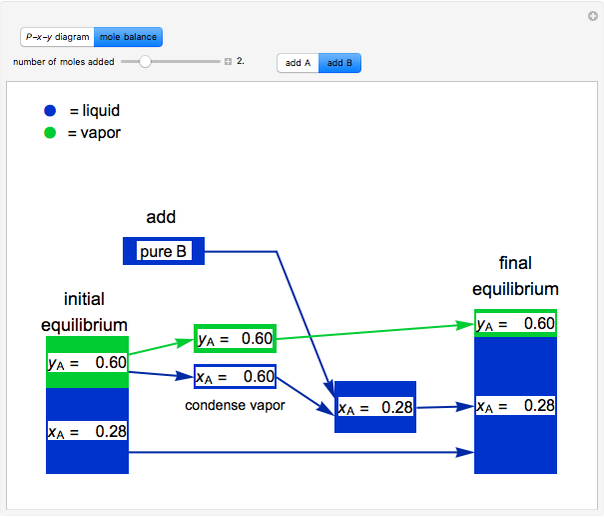
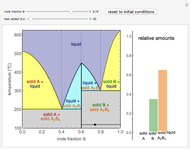
and 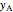 do not change. Select "mole balance" to see how this is possible. The size of a rectangle is proportional to the amount of that phase (blue is liquid, green is vapor). For example, adding
do not change. Select "mole balance" to see how this is possible. The size of a rectangle is proportional to the amount of that phase (blue is liquid, green is vapor). For example, adding  increases the vapor-to-liquid ratio, so some of the initial liquid vaporizes, and this amount is determined by a mass balance. For ease of visualization,
increases the vapor-to-liquid ratio, so some of the initial liquid vaporizes, and this amount is determined by a mass balance. For ease of visualization,  is shown being added as a vapor and
is shown being added as a vapor and  as a liquid, but the final equilibrium is the same if
as a liquid, but the final equilibrium is the same if  is added as a liquid and
is added as a liquid and  as a vapor because the system is isothermal. For example, if pure
as a vapor because the system is isothermal. For example, if pure  were added as a liquid, it would vaporize to satisfy the mass balances.
were added as a liquid, it would vaporize to satisfy the mass balances.
Contributed by: Rachael L. Baumann and Megan Maguire (October 2014)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The pressure-composition 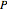 -
- -
- diagram was made using Raoult's law:
diagram was made using Raoult's law:
 ,
,
 ,
,
where  and
and 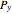 are the bubble and dew curves (bar),
are the bubble and dew curves (bar),  is the mole fraction of
is the mole fraction of  in the initial mixture with
in the initial mixture with 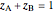 and
and  is the saturation pressure calculated from the Antoine equation:
is the saturation pressure calculated from the Antoine equation:
 ,
,
where  ,
,  and
and 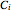 are Antoine constants.
are Antoine constants.
The lever rule is used to calculate the amount of liquid and vapor present at an overall composition of  :
:
amount of liquid =  ,
,
amount of vapor =  ,
,
where 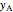 is the vapor mole fraction of
is the vapor mole fraction of  , and
, and 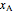 is the liquid mole fraction of
is the liquid mole fraction of  .
.
The screencast video at [1] explains how to use this Demonstration.
Reference
[1] Mass Balances for Binary Vapor-Liquid Equilibrium (VLE) [Video]. (Oct 12, 2016) www.colorado.edu/learncheme/thermodynamics/MassBalanceBinaryVLE.html.
Permanent Citation