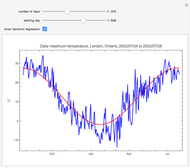
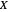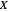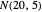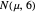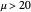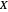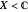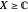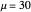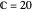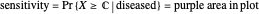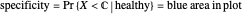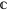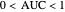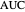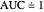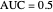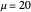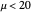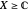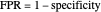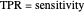How Receiver Operating Characteristic Curves Work

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
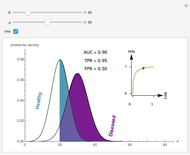
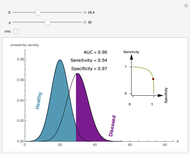
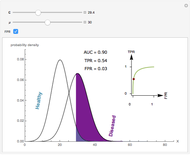
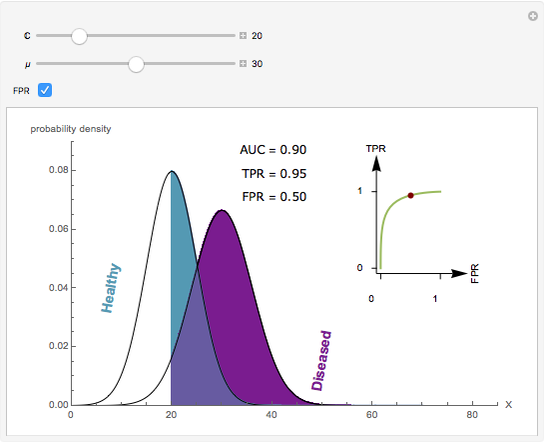
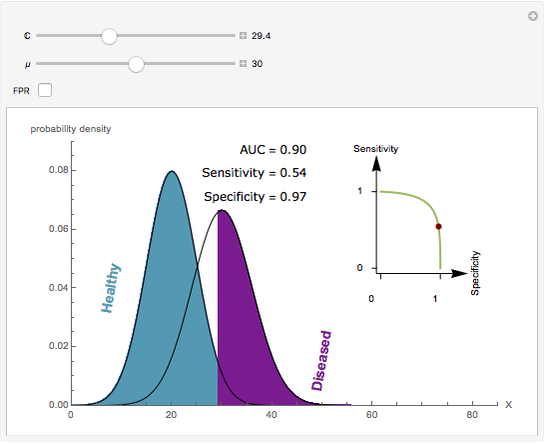
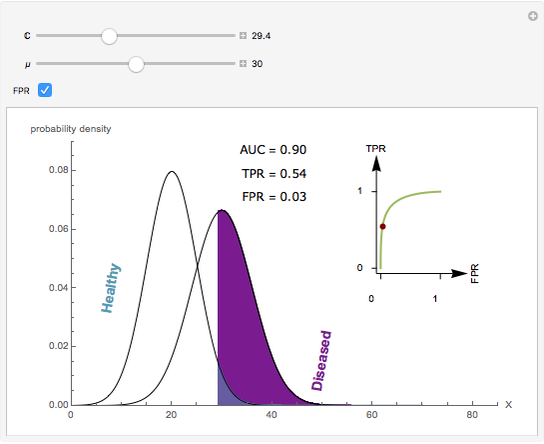
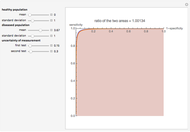
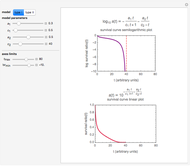
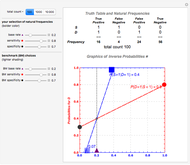
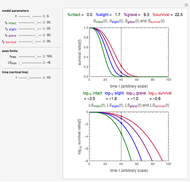
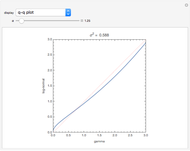
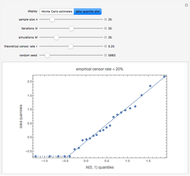
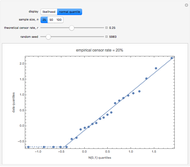
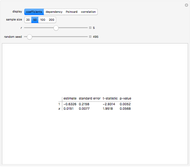
Visually the ROC curve, shown in the top-right corner, is the shaded area under the right curve versus the shaded area under the left curve as the threshold parameter 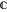 varies. A more detailed explanation now follows.
varies. A more detailed explanation now follows.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
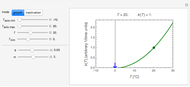
Denote the cumulative distribution functions of 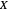 in the healthy and diseased populations by
in the healthy and diseased populations by 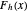 and
and 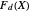 . Then the tail functions are respectively
. Then the tail functions are respectively 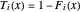 ,
, 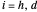 . It may be shown that
. It may be shown that 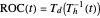 ,
, 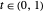 and
and
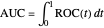 .
.
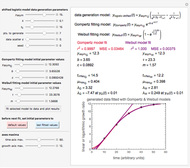
An explicit closed-form formula for AUC in the case of binormal populations is given in [1], p. 34.
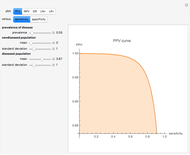
The AUC can be interpreted as the probability that a randomly chosen member from the diseased population will have a higher 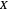 than a randomly chosen member from the healthy population.
than a randomly chosen member from the healthy population.
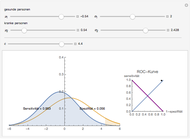
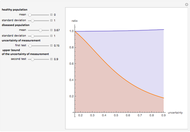
An interesting example of the use of ROC curves to compare classifiers is given in [2], figure 9.6, p. 316. See also the Demonstration "Uncertainty of Measurement and Diagnostic Accuracy Measures" for an illustration of the use of ROC to compare two diagnostic tests. In practice, ROC curves are often used to compare a number of diagnostic tests or classifiers.
The glaucoma example discussed in this Demonstration is presented in [4] and there are many similar examples in the references below. Two in-depth treatments of ROC curves are provided in [1] and [3].
[1] W. J. Krzanowski and D. J. Hand, ROC Curves for Continuous Data, CRC/Chapman & Hall, 2009.
[2] T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed., New York: Springer, 2009.
[3] M.S. Pepe, The Statistical Evaluation of Medical Tests for Classification and Prediction, New York: Oxford, 2003.
[4] J. A. Swets, R. M. Dawes, and J. Monahan, "Better Decisions through Science," Scientific American, 283, 2000 pp. 82–87.
Permanent Citation