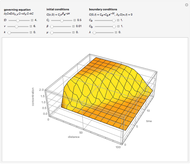
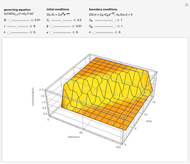
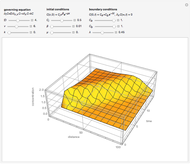
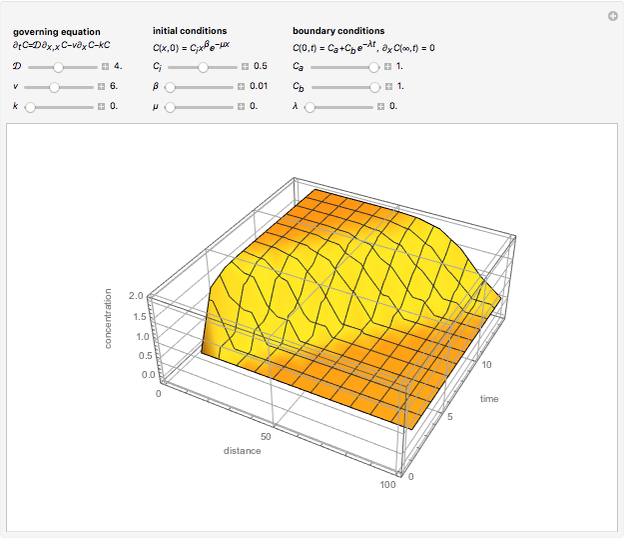
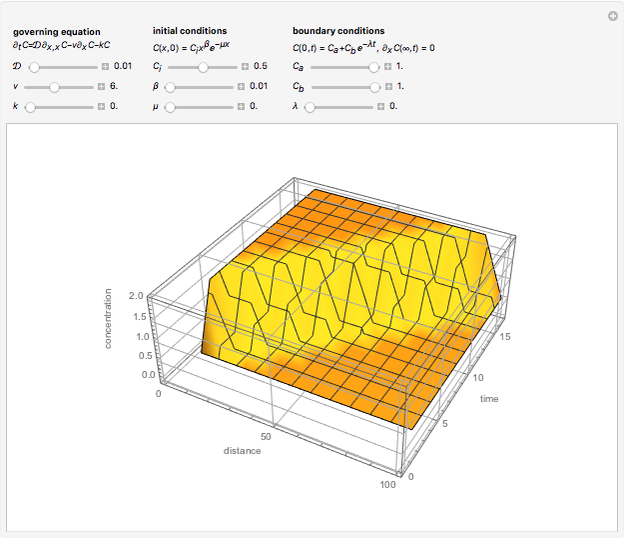
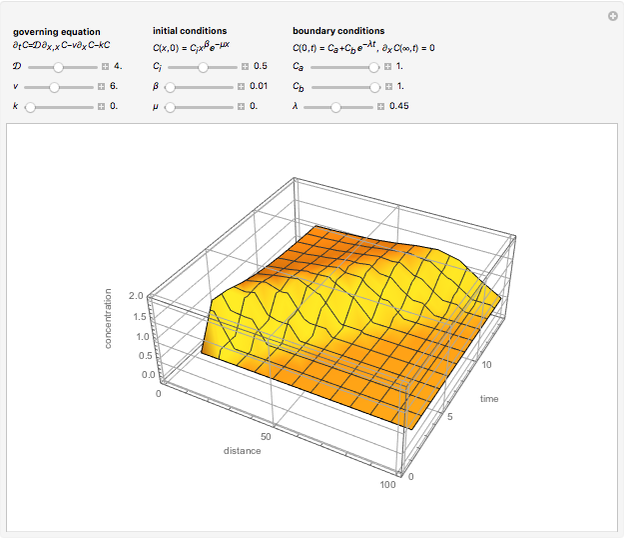
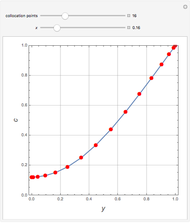
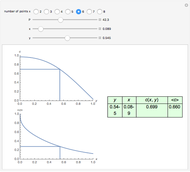
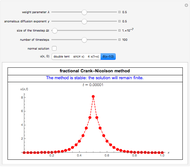
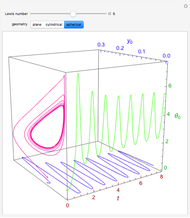
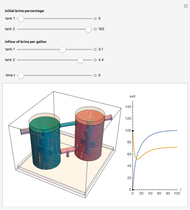
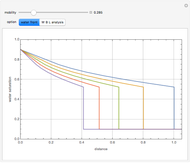
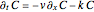The mixing cell model is used to solve the diffusion-advection equation with complex initial and boundary conditions.
The equation describing the one-dimensional transport of a reacting component in porous media is
 ,
,
where  is the fluid phase concentration,
is the fluid phase concentration,  is the effective dispersion coefficient,
is the effective dispersion coefficient,  is distance,
is distance,  is time,
is time,  is the interstitial fluid velocity, and
is the interstitial fluid velocity, and  is a reaction constant. A function similar to the gamma distribution is used as the initial condition, and a time-dependent boundary condition is applied at
is a reaction constant. A function similar to the gamma distribution is used as the initial condition, and a time-dependent boundary condition is applied at  .
.
 ,
,
 , and
, and
 .
.
Here  ,
,  ,
,  ,
,  ,
,  , and
, and  are constants.
are constants.
The mixing cell model is an explicit finite-difference approximation to the diffusion-advection equation in which the dispersion term is neglected and a pure advection equation given by 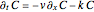 is solved.
is solved.
Finite-difference solutions of this equation can produce numerical dispersion, which is controlled to simulate solutions to the advection-diffusion equation [1]. The time derivative is approximated with a forward difference, while a backward difference is used to approximate the space derivative. For the  cell, this approximation is written as
cell, this approximation is written as
 .
.
The numerical dispersion introduced is  .
.
To solve the advection-diffusion equation, this numerical dispersion is equated to the physical dispersion coefficient  . Thus for any choice of
. Thus for any choice of  ,
,  . This model greatly simplifies the computation, making solutions for complex convective-dispersive phenomena possible; complexities such as additional transport phenomena, chemical reactions, or flow profiles can be added to the cell model without changing its mathematical form or markedly increasing the difficulty of obtaining solutions.
. This model greatly simplifies the computation, making solutions for complex convective-dispersive phenomena possible; complexities such as additional transport phenomena, chemical reactions, or flow profiles can be added to the cell model without changing its mathematical form or markedly increasing the difficulty of obtaining solutions.
[less]