Model of Immune Response with Time-Dependent Immune Reactivity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
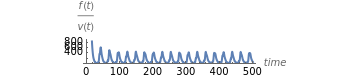
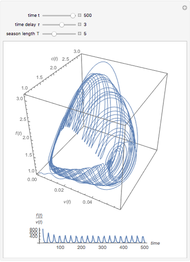
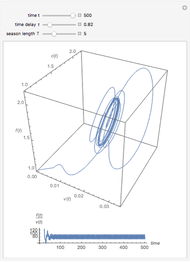
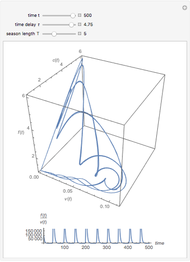
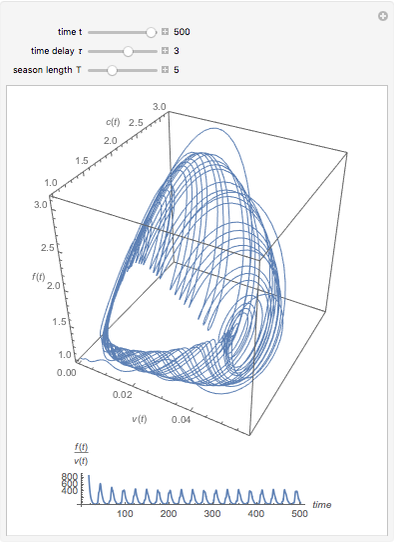
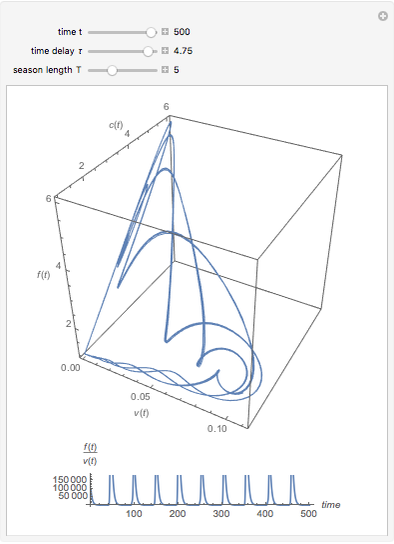
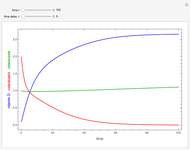
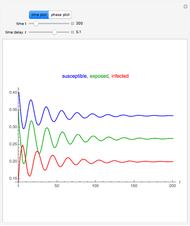
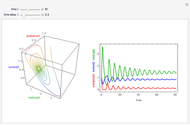
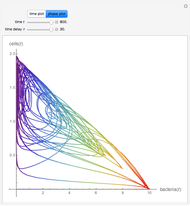
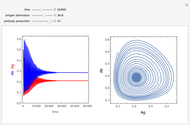
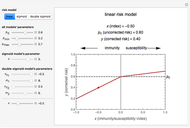
The probability of getting a disease is related to the efficiency of the immune system, which can change with the seasons of the year. This Demonstration shows the solution of a model of the immune system that has periodic changes in the immune reactivity due to changes in the environment.
[more]
Contributed by: Clay Gruesbeck (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] M. Bodnar and U. Fory\:015b, "A Model of Immune System with Time-Dependent Immune Reactivity," Nonlinear Analysis, 70(2), 2009 pp. 1049–1058. doi:10.1016/j.na.2008.01.031.
Permanent Citation