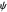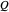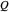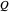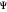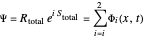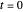The relevant Hilbert space for the wavefunction in quantum mechanics is an infinite-dimensional vector space. But the nature and the physical significance (the ontology) of a complex-valued wavefunction is problematic: at each point in space and time, the wavefunction is described by a complex number.
[more]
The squared magnitude of the wavefunction is generally considered physically significant, representing a conceptually observable wave or probability amplitude. But there is more to the wavefunction. A speculative approach based on a combination of the de Broglie–Bohm interpretation (Bohmian mechanics) is given in Eugene Khutoryansky's video [1]. In de Broglie–Bohm theory, the particle has a well-defined trajectory in configuration space, calculated from the gradient of the total phase function that is guided by the 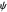 field via the quantum potential
field via the quantum potential 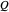 . The de Broglie–Bohm ontology is a deterministic and causal theory in contrast of the conventional (Copenhagen) interpretation of quantum mechanics [2–5].
. The de Broglie–Bohm ontology is a deterministic and causal theory in contrast of the conventional (Copenhagen) interpretation of quantum mechanics [2–5].
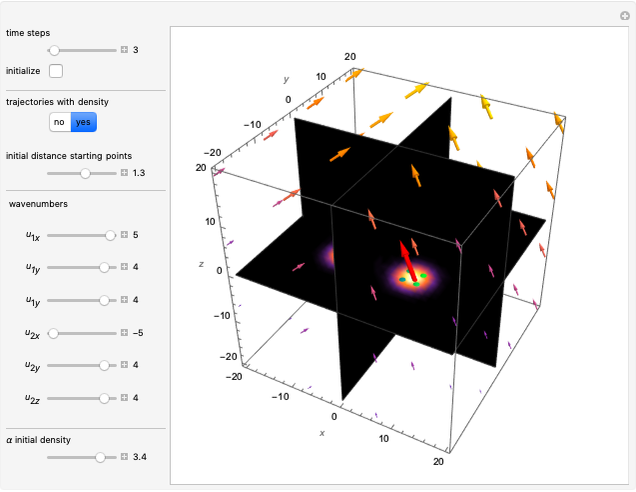
All complex numbers have a real component and an imaginary component. For a one-dimensional wavefunction with a time-dependent phase, the wavefunction rotates around the  axis. A quantum particle with a higher wavenumber has a wavefunction that rotates with a higher frequency, which is calculated from the total phase of the wavefunction in polar form. The frequency of the wavefunction determines the energy of the particle. The momentum of the quantum particle is determined by the wavelength, here described by the wave number
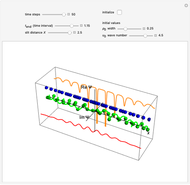
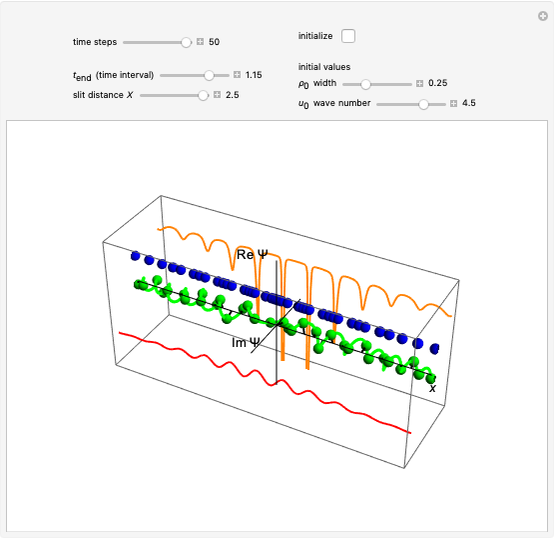
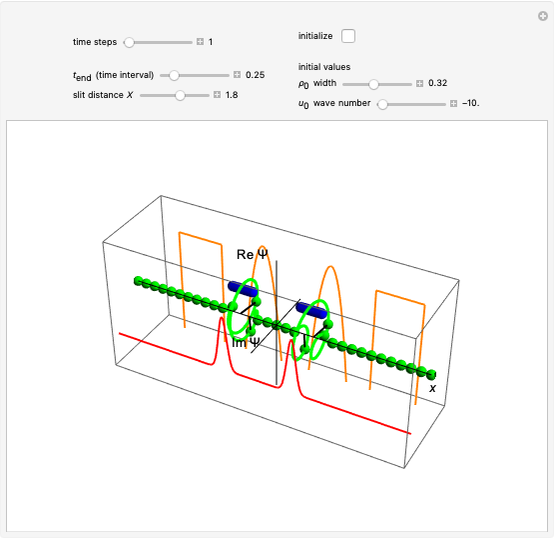
axis. A quantum particle with a higher wavenumber has a wavefunction that rotates with a higher frequency, which is calculated from the total phase of the wavefunction in polar form. The frequency of the wavefunction determines the energy of the particle. The momentum of the quantum particle is determined by the wavelength, here described by the wave number  . In this Demonstration, the total wavefunction is in a superposition state of two free particles described by two unnormalized Gaussian wave profiles, analogous to the case of the two-slit experiment [2]. The free particles have the same initial width and the same wave number
. In this Demonstration, the total wavefunction is in a superposition state of two free particles described by two unnormalized Gaussian wave profiles, analogous to the case of the two-slit experiment [2]. The free particles have the same initial width and the same wave number  , but opposite signs.
, but opposite signs.
In David Bohm's causal interpretation of quantum mechanics, the wavefunction in a complex Hilbert space has objective reality. It provides a complete description of the system, describing an observer-independent reality leading to precisely the same results as does the usual interpretation. The 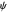 field exerts a force via the quantum potential
field exerts a force via the quantum potential 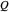 on the particle in a way that is analogous but not identical to the way an electromagnetic field exerts a force on a charge. The main differences are that the quantum potential
on the particle in a way that is analogous but not identical to the way an electromagnetic field exerts a force on a charge. The main differences are that the quantum potential 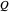 does not depend on the intensity of the wave, but rather on its form; it need not fall off with increasing distance. Another important difference is that, because of the homogeneous structure of the
does not depend on the intensity of the wave, but rather on its form; it need not fall off with increasing distance. Another important difference is that, because of the homogeneous structure of the  field, it is not radiated or absorbed when it interacts with particles [3].
field, it is not radiated or absorbed when it interacts with particles [3].
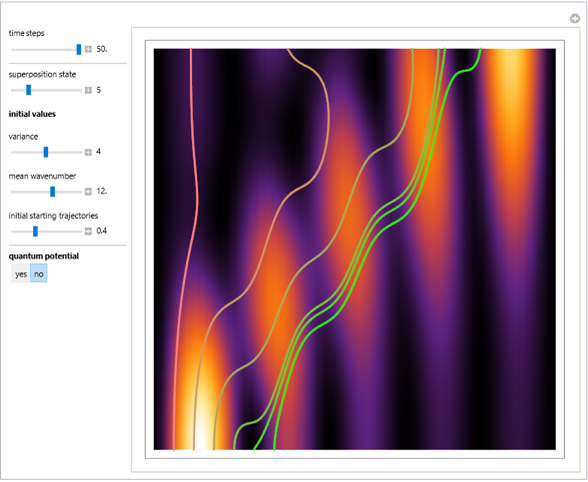
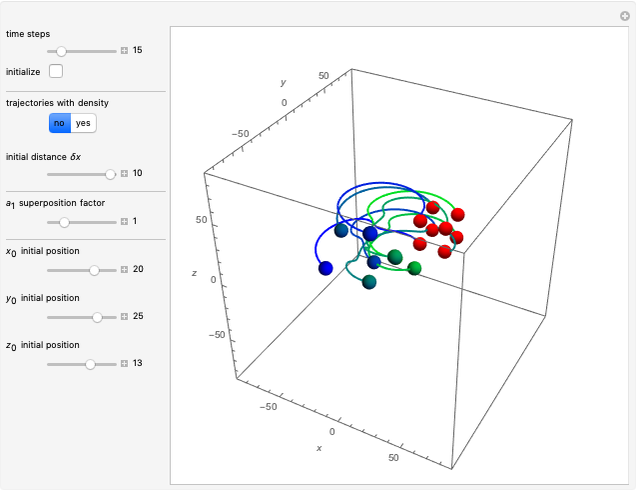
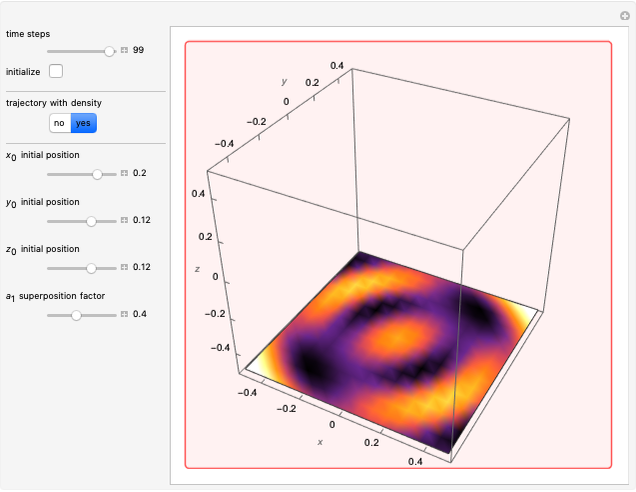
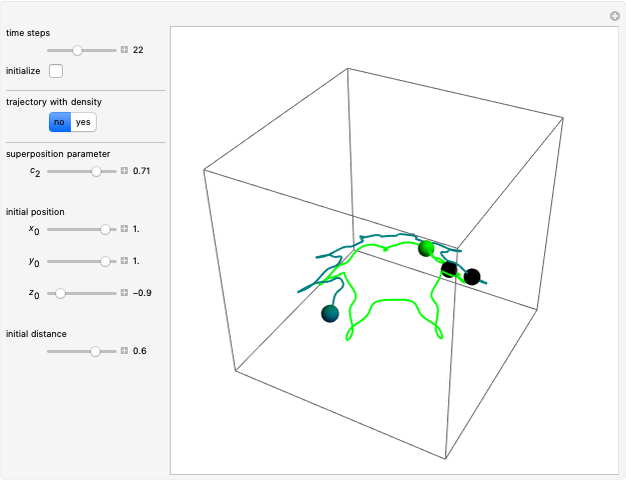
The actual possible positions of the particles run to the local maxima of the squared wavefunction and therefore correspond to the bright fringes of the diffraction pattern. They do not cross or pass through nodes.
The position and motion of a particle are obtained by integrating the gradient of the real phase function, using the total wavefunction 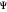 in the eikonal representation:
in the eikonal representation:
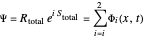 .
.
In this speculative approach, the hidden variables are the wavefunction itself and the initial positions of the free particles in the wave density at time 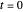 .
.
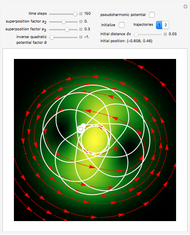
The graphics show the real and imaginary parts of the wavefunction (green), the wave density (red), the quantum potential (orange) and the actual position of 50 possible particles (blue). The plot of the quantum potential is scaled to fit.
[less]
Details
An unnormalized wavefunction 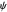 for one-dimensional free particles, from which the actual positions are calculated, can be defined by a superposition state in atomic units:
for one-dimensional free particles, from which the actual positions are calculated, can be defined by a superposition state in atomic units:

with the wave number  , initial width
, initial width  and slit distance
and slit distance 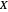 .
.
In the eikonal representation (often called the polar form) 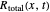 and
and 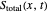 are calculated from:
are calculated from:
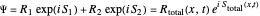
with
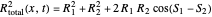
and
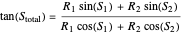 .
.
In a more explicit form:
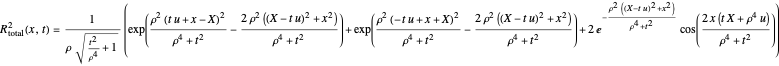
and
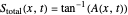 ,
,
with
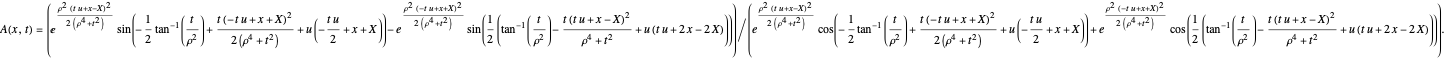
The real and the imaginary components of the wavefunction arise from:

and
 .
.
According to the conventional Copenhagen interpretation, the measured intensity 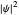 takes the form
takes the form
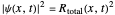 .
.
The quantum potential 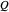 is given by:
is given by:
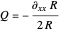
with the partial derivation 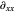 with respect to
with respect to 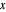 .
.
In the code, increase PlotPoints, AccuracyGoal, PrecisionGoal and MaxSteps for accurate results.
References
[1] E. Khutoryansky, "Quantum Wave Function Visualization" [Video]. (Nov. 12, 2020) www.youtube.com/watch?v=KKr91v7yLcM&t=368s.
[2] C. Philippidis, C. Dewdney and B. J. Hiley, "Quantum Interference and the Quantum Potential," Il Nuovo Cimento B, 52(1), 1979 pp. 15–28. doi:10.1007/BF02743566.
[3] D. Bohm, "A Suggested Interpretation of the Quantum Theory in Terms of 'Hidden' Variables. (I, II)," Physical Review, 85(2), 1952 pp. 166–193. doi:10.1103/PhysRev.85.166 and doi:10.1103/PhysRev.85.180.
[4] Bohmian-Mechanics.net. (Nov. 12, 2020) bohmian-mechanics.net.
[5] S. Goldstein, "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy (Summer 2017 Edition). (Nov. 12, 2020) plato.stanford.edu/entries/qm-bohm.

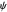 for one-dimensional free particles, from which the actual positions are calculated, can be defined by a superposition state in atomic units:
for one-dimensional free particles, from which the actual positions are calculated, can be defined by a superposition state in atomic units: 
 , initial width
, initial width  and slit distance
and slit distance 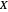 .
.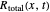 and
and 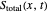 are calculated from:
are calculated from: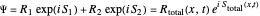
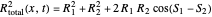
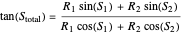 .
.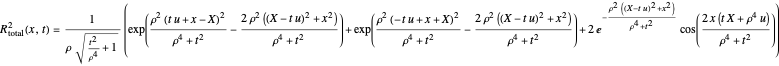
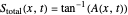 ,
,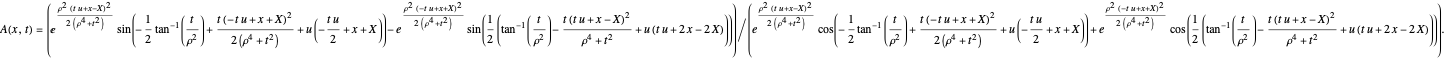

 .
.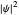 takes the form
takes the form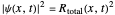 .
. 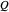 is given by:
is given by: 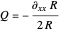
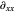 with respect to
with respect to 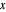 .
.