Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

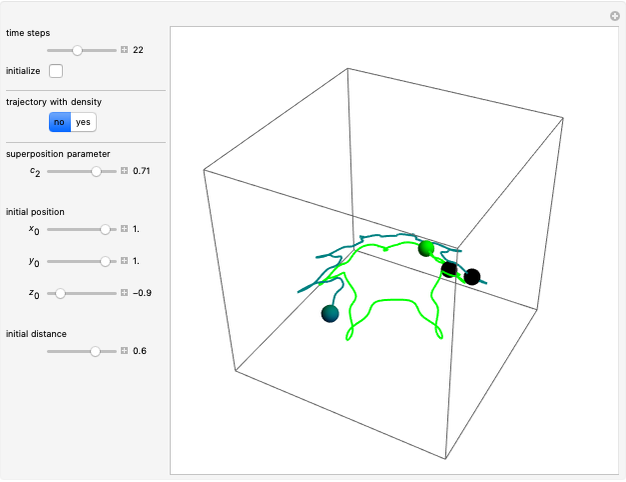
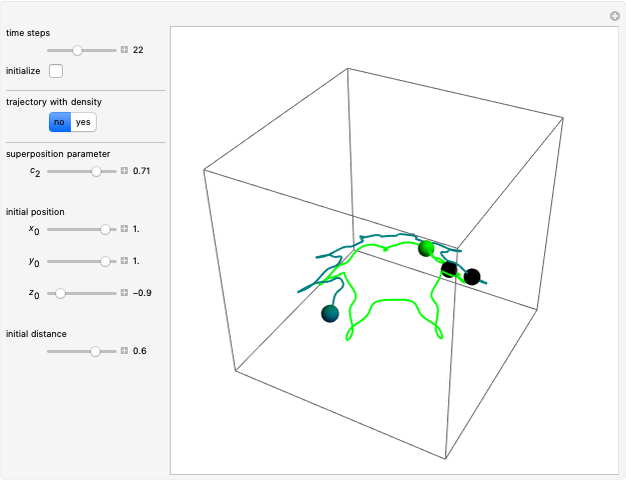
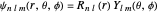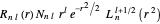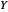Quantum Orbits of a Particle in Spherical Coordinates in a Three-Dimensional Harmonic Oscillator Potential

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

The isotropic three-dimensional harmonic oscillator in spherical polar coordinates is described by the Schrödinger equation

[more]

,

in atomic units [1], here, such that . The normalized solution is separable:

,

with the radial function

and with the normalization constant

,

where is an associated Laguerre polynomial, is a spherical harmonic and is a normalization constant.

In the de Broglie–Bohm (or causal) interpretation of quantum mechanics [2, 3], the particle position and momentum are well defined and the motion can be described by continuous evolution according to the time-dependent Schrödinger equation.

The dynamic behavior for such a system is quite complex. Some of the curves are closed and periodic, while others are quasi-periodic. Chaos is generated when an orbit approaches an unstable region in the neighborhood of a nodal point or nodal line [4] where the wavefunction vanishes and the trajectories apparently become strongly accelerated. Here, chaotic motion means the exponential divergence of initially neighboring trajectories. The initial positions have to be chosen carefully because of the singularities in the velocities and the resulting large oscillations, which can lead to very unstable trajectories. The quantum motion originates from the relative phase of the total wavefunction, which has no analog in classical particle mechanics. Further investigation to capture the full dynamics of the system is necessary.

The graphics show three-dimensional contour plots of the squared wavefunction (if enabled) and two initially neighboring possible trajectories of one particle. Black spheres mark the initial positions of the two quantum particles and green spheres the actual positions.

[less]

Contributed by: Klaus von Bloh (February 2019)
Open content licensed under CC BY-NC-SA

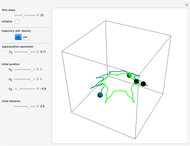
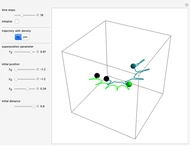
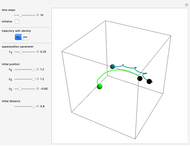
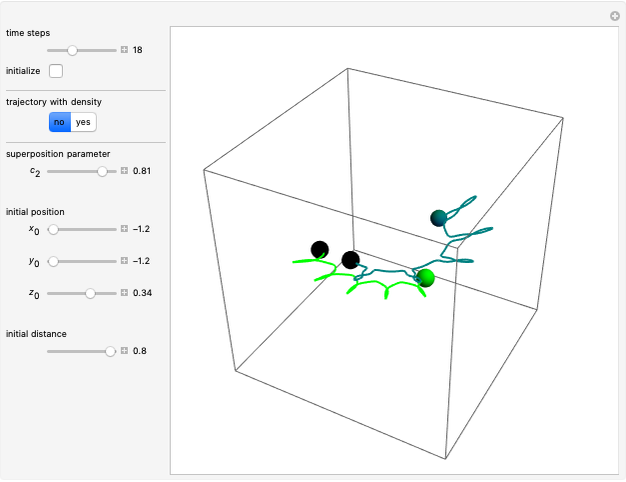
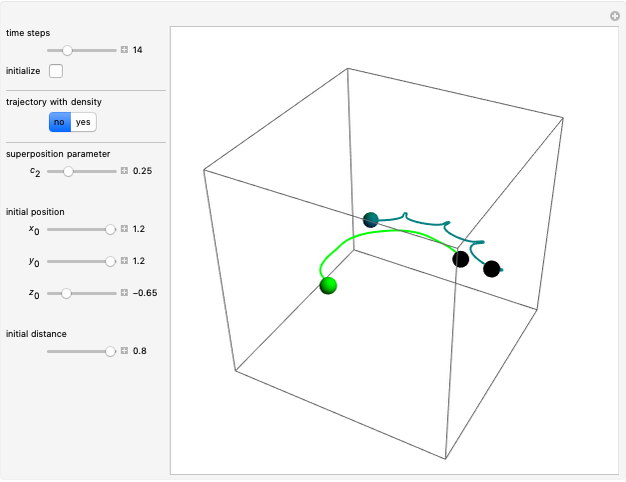
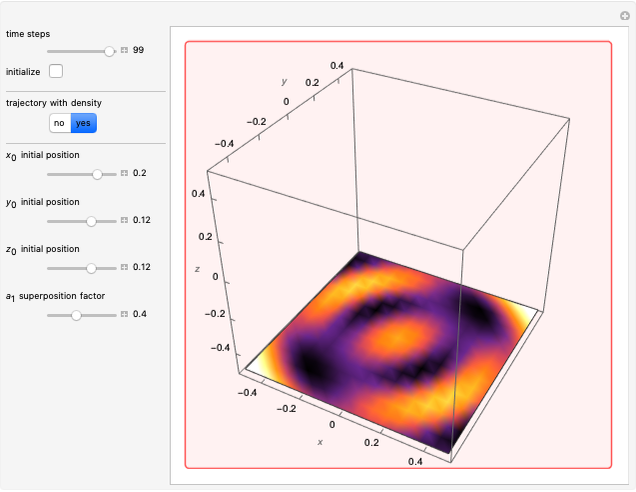
Snapshots

Details

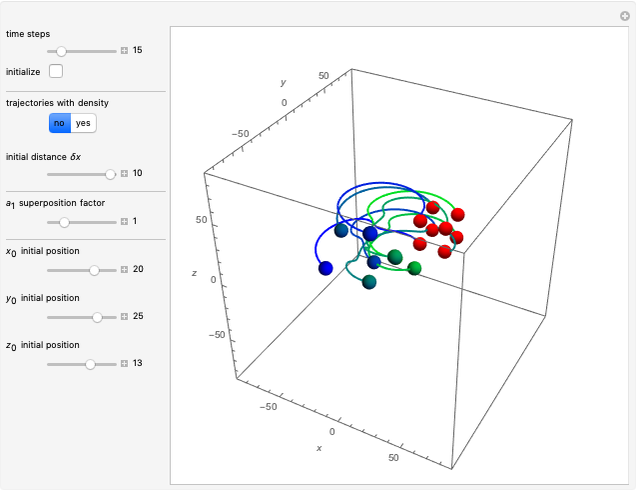
In this Demonstration, the total wavefunction 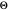is defined by a superposition of two eigenstates:

,

with 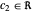and .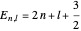

In this case, the wavefunction for the harmonic oscillator in spherical polar coordinates [4] reads

.

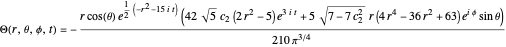The velocity field 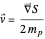is calculated from the gradient of the phase from the total wavefunction in the eikonal form (often called polar form) . The time-dependent phase function from the total wavefunction is

.

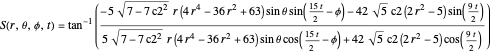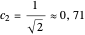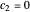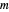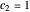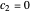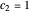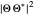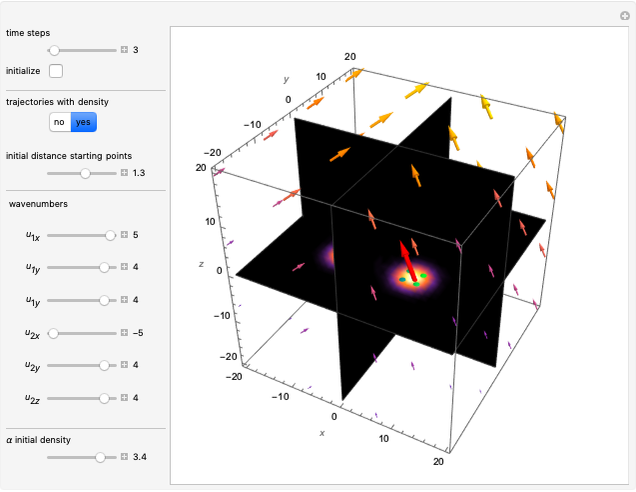
For , both initial states are weighted equally. Since the wavefunction is in the single initial state with , the orbits of the particles are circles because of the magnetic quantum number , and for , the particles are at rest. For these stationary states such as for and , the distribution with the complex conjugate 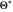is a constant of time; that is, it does not change. For and for 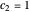, the distributions 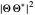are

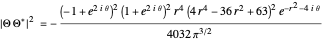
and

,

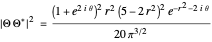respectively.

In Cartesian coordinates with

,

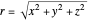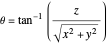
and

,

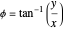the total wavefunction combines to

.

With a little more effort, it could be shown that the wavefunctions in spherical coordinates are just linear combinations of the solutions in Cartesian coordinates.

The normalization condition for the total wavefunction of 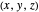yielding a result between 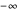and is defined by

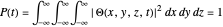
because if the position of the particle is measured, there is 100% probability that it will be somewhere.

In the program, if PlotPoints, AccuracyGoal, PrecisionGoal, MaxSteps and MaxIterations are enabled, increasing them will give more accurate results.

References

[1] Wikipedia. "Atomic Units." (Feb 26, 2019) en.wikipedia.org/wiki/Atomic_units.

[2] Bohmian-Mechanics.net. (Feb 26, 2019) www.bohmian-mechanics.net/index.html.

[3] S. Goldstein, "Bohmian Mechanics," The Stanford Encyclopedia of Philosophy, Summer 2017 Edition (E. N. Zalta, ed.), (Feb 26, 2019)plato.stanford.edu/archives/sum2017/entries/qm-bohm.

[4] A. C. Tzemos, C. Efthymiopoulos and G. Contopoulos, "Origin of Chaos Near Three-Dimensional Quantum Vortices: A General Bohmian Theory," Physical Review E, 97(4), 2018 pp. 042201-1–042201-13. doi:10.1103/PhysRevE.97.042201. arxiv.org/abs/1803.08613v1.

[5] Wikipedia. "Quantum Harmonic Oscillator." (Feb 26, 2019) en.wikipedia.org/wiki/Quantum_harmonic_oscillator.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send