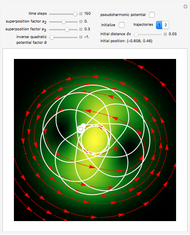
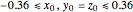Quantum Motion in an Infinite Spherical Well

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
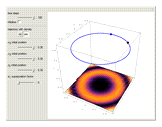
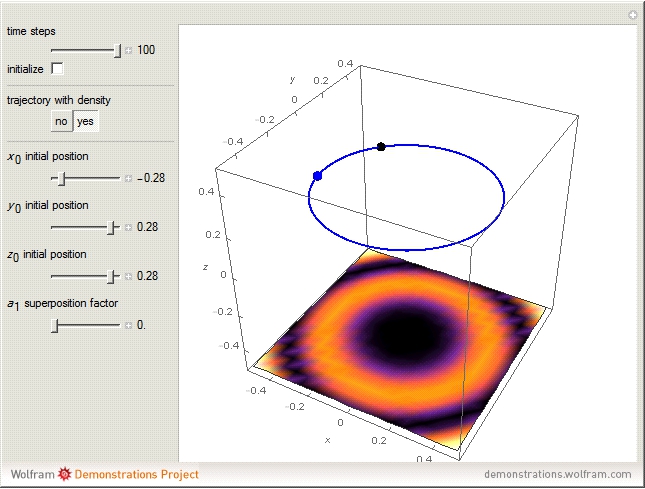
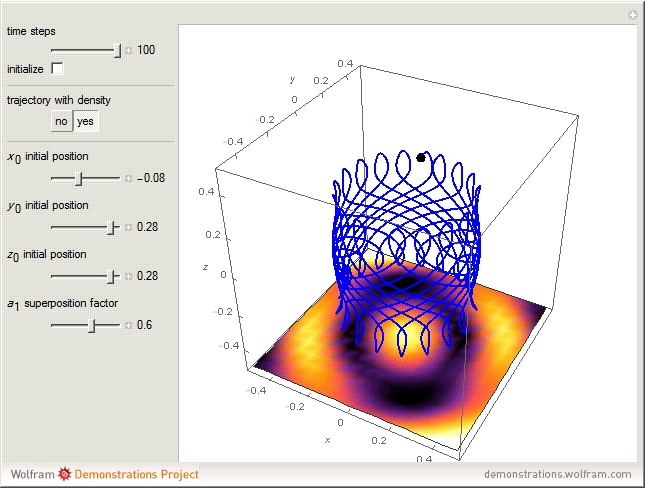
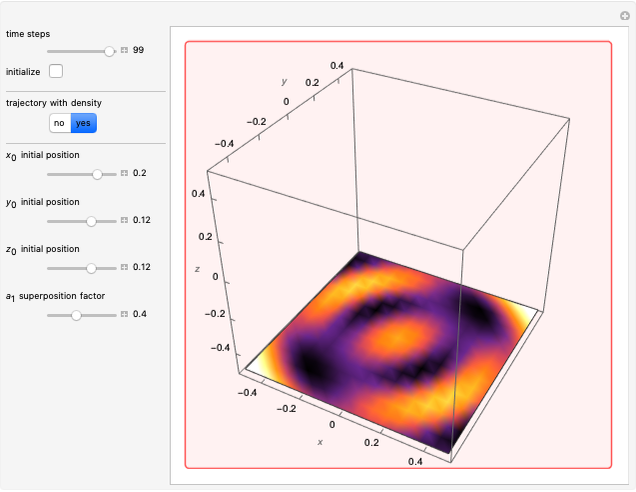
Quantum billiards are an important class of systems showing a large variety of dynamical behavior ranging from regular motion through quasiperiodic behavior to strongly chaotic behavior. Suppose a single quantum particle, an atom, is in a superposition of two energy eigenstates, in the absence of measurement. This could be achieved by exciting the atom with coherent laser pulses. For this system, a transformation from regular to quasiperiodic motion is shown in the Bohm trajectories for this "unobserved" system. If, before emitting a photon, a position or energy measurement is made, the atom will remain in the superposition state.
[more]
Contributed by: Klaus von Bloh (October 2019)
Open content licensed under CC BY-NC-SA
Details
An unnormalized wavefunction  of the Schrödinger equation
of the Schrödinger equation

with mass 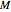 is separable in spherical polar coordinates, such that
is separable in spherical polar coordinates, such that
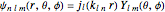 ,
,
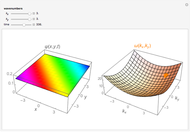
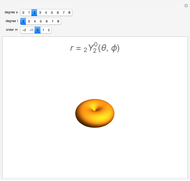
where  is a spherical harmonic and
is a spherical harmonic and 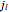 a spherical Bessel function [3]. The boundary condition that
a spherical Bessel function [3]. The boundary condition that  at
at 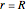 is fulfilled when
is fulfilled when 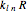 is the
is the 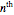 zero of the spherical Bessel function
zero of the spherical Bessel function 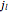 . The quantized energy levels are then given by
. The quantized energy levels are then given by
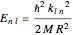 ,
,
where 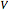 is the central potential energy with
is the central potential energy with
 .
.
In this Demonstration, the total wavefunction  is defined by a superposition of two stationary eigenstates:
is defined by a superposition of two stationary eigenstates:
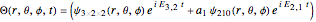
with 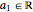 .
.
For simplicity, set the mass 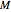 and
and  equal to 1 (atomic units [4]).
equal to 1 (atomic units [4]).
In this case, the wavefunction for the quantum particle in an infinite spherical well in spherical polar coordinates [1] reads
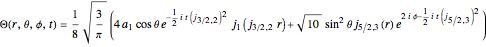 .
.
The velocity field  with the position
with the position 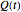 can be calculated from the current
can be calculated from the current 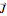
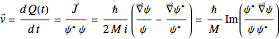
or from the gradient of the total phase function 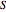 from the wavefunction
from the wavefunction  in the eikonal form (often called polar form)
in the eikonal form (often called polar form) 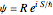 :
:
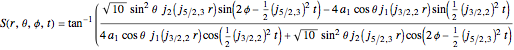 .
.
From the total phase function 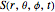 the gradient
the gradient  , with the partial derivative
, with the partial derivative 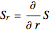 and so on, is given by:
and so on, is given by:
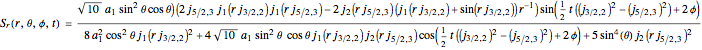 ,
,
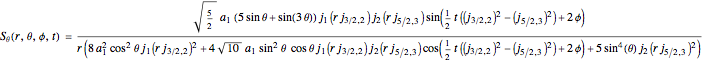
and
 .
.
For the initial point 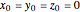 the velocity becomes indeterminate, and for
the velocity becomes indeterminate, and for 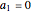 the velocity field
the velocity field  becomes autonomous, with
becomes autonomous, with
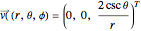 ,
,
or in Cartesian coordinates,
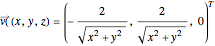 ,
,
and the atom orbits the  axis along a circle of constant radius and with a constant angular speed depending on the azimuthal quantum number
axis along a circle of constant radius and with a constant angular speed depending on the azimuthal quantum number  (here,
(here, 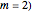 , which is a multiple of
, which is a multiple of
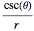 or
or 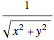 .
.
For greater accuracy, increase PlotPoints, AccuracyGoal, PrecisionGoal and MaxSteps.
Due to the computational limitations, here only two superposed states are investigated. For this case, there is no chaotic behavior in the quantum motion [5, 6].
References
[1] Bohmian-Mechanics.net. (Oct 18, 2019)
[2] S. Goldstein, "Bohmian Mechanics," The Stanford Encyclopedia of Philosophy, Summer 2017 Edition (E. N. Zalta, ed.), (Oct 24, 2019)plato.stanford.edu/archives/sum2017/entries/qm-bohm.
[3] O. F. de Alcantara Bonfim, J. Florencio and F. C. Sá Barreto, "Chaotic Bohm’s Trajectories in a Quantum Circular Billiard," Physics Letters A, 277(3), 2000 pp. 129–134. doi:10.1016/S0375-9601(00)00705-2.
[4] Wikipedia. "Hartree Atomic Units." (Oct 18, 2019) en.wikipedia.org/wiki/Atomic_units.
[5] R. H. Parmenter and R. W. Valentine, "Deterministic Chaos and the Causal Interpretation of Quantum Mechanics," Physics Letters A, 201(1), 1995 pp. 1–8. doi:10.1016/0375-9601(95)00190-E.
[6] R. H. Parmenter and R. W. Valentine, "Erratum: Deterministic Chaos and the Causal Interpretation of Quantum Mechanics (Physics Letters A 210 (1995) 1)," Physics Letters A, 213(5–6), 1996 p. 319. doi:10.1016/0375-9601(96)00096-5.
Snapshots
Permanent Citation