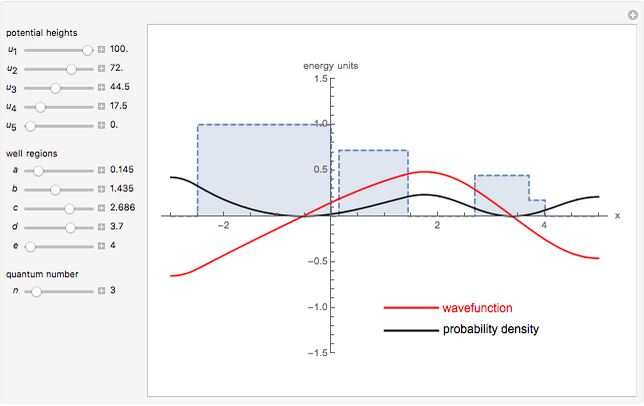
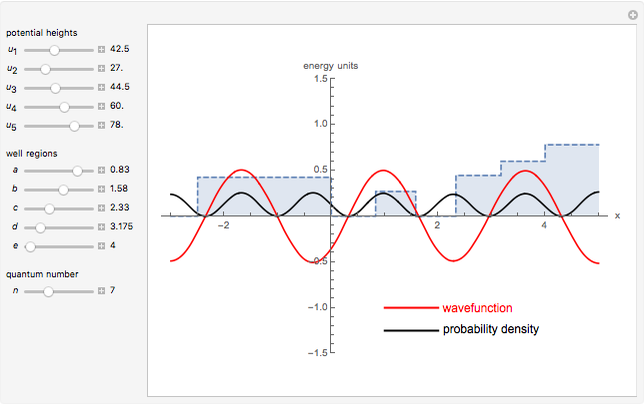
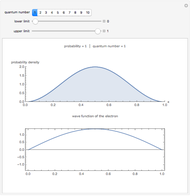
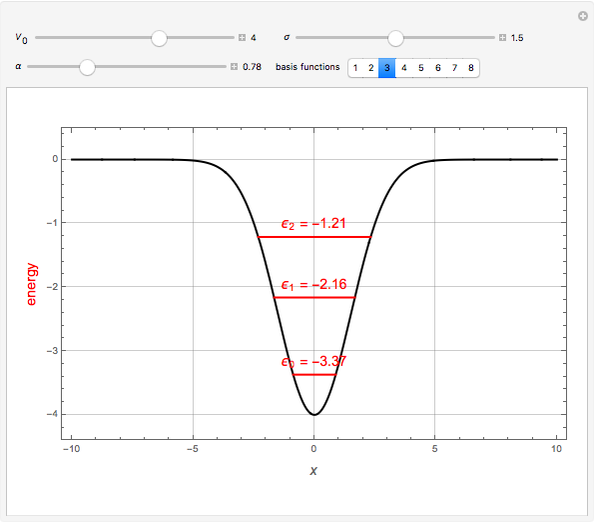
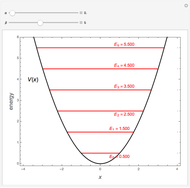
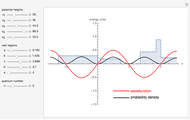
This Demonstration shows solutions of the one-dimensional Schrödinger equation in a multi-step potential well, confined between 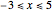. The controls on the left determine the heights and widths of the segments of the potential well. Select a quantum number (from 1 to 20) to plot the 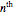eigenfunction of the Schrödinger equation . The Schrödinger equation is then solved numerically using Mathematica's built-in function NDEigensystem. Energies are expressed in units of 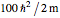. The wavefunctions are plotted in red, in arbitrary units, with the black curves showing the corresponding probability densities.