Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Reducing a Differential Equation of a Special Form to a Homogeneous Equation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

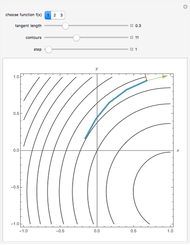
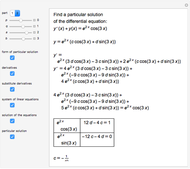
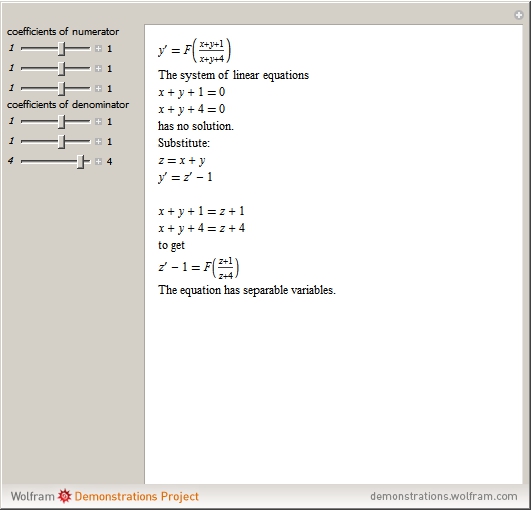
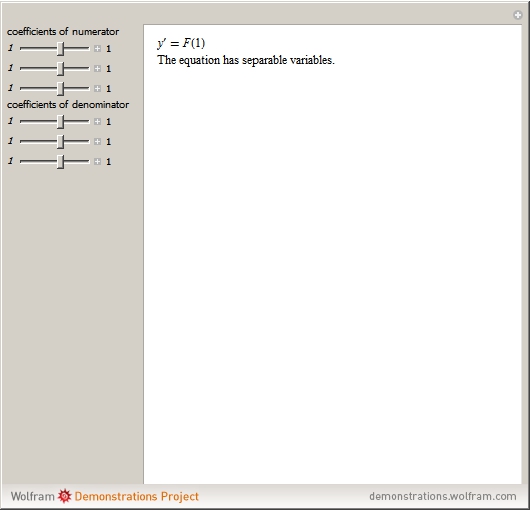
This Demonstration shows the reduction of a differential equation of the form to a homogeneous differential equation of the form . This case occurs if the system of linear equations , has a unique solution , ; then new variables are introduced by the equations , . If the system of linear equations has no solution or has infinitely many solutions, the differential equation reduces to an equation with separable variables.

Contributed by: Izidor Hafner (May 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The equation is called homogeneous if and are homogeneous functions of of the same order. The equation can be reduced to the form . A function is called homogeneous of order if . An example: and are homogeneous of order 2, and is homogeneous of order 0.

The differential equation is not homogeneous in the usual sense of a linear differential equation having a right-hand side equal to zero, like .

References

[1] V. I. Smirnoff, Lectures in Higher Mathematics (in Russian), Vol. 2, Moscow: Nauka, 1967 pp. 19–21.

[2] L. E. Eljsgoljc, Differential Equations and Variational Calculus (in Russian), Moscow: Nauka 1969 pp. 26–27.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send