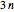Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Richardson Extrapolation Applied Twice to Accelerate the Convergence of an Estimate

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

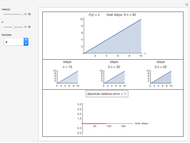
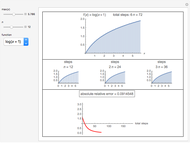
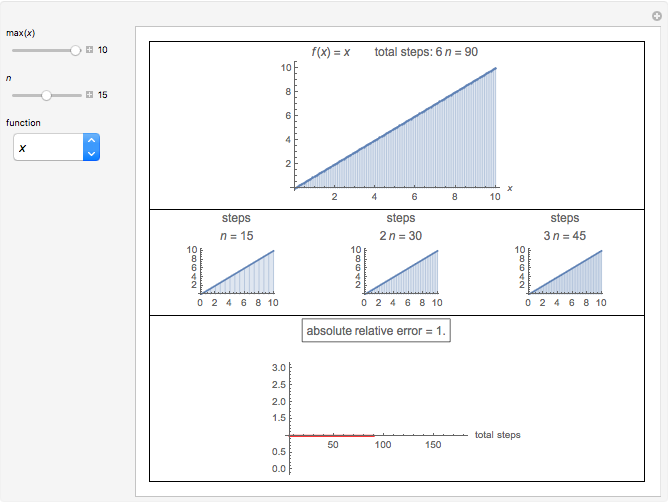
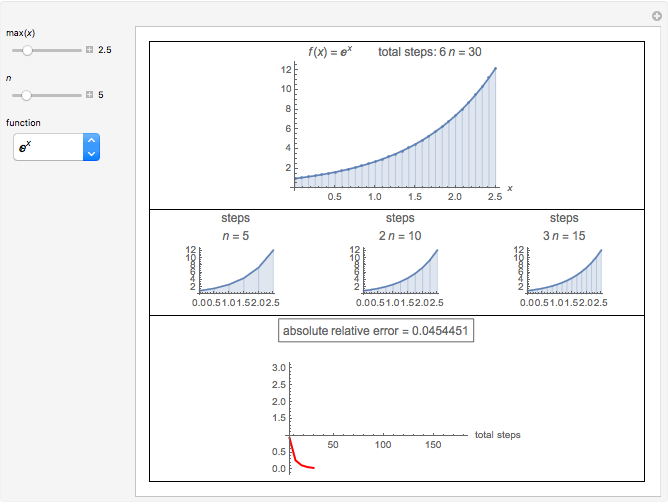
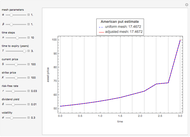
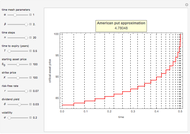
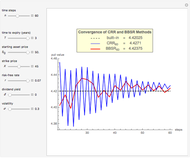
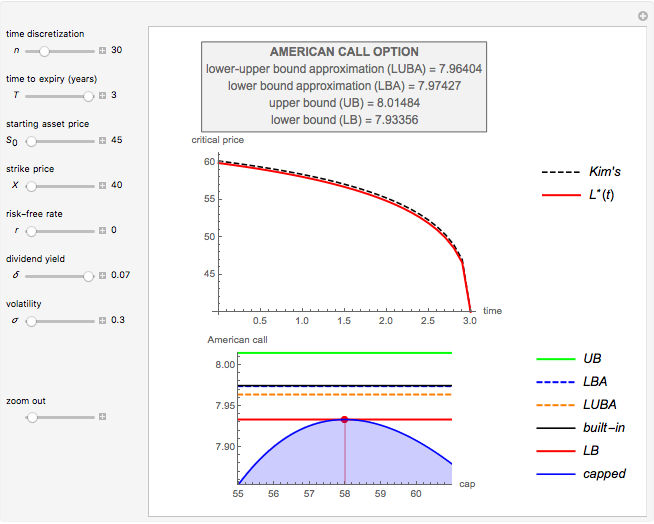
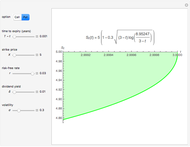
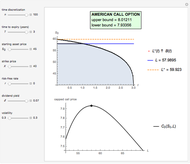
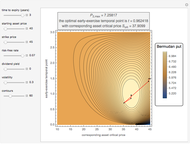
This Demonstration shows Richardson extrapolation applied twice to accelerate the convergence of an estimate.

[more]

• top graph: select a function and a desired discretization in order to estimate the function's integral with the trapezoidal rule, using a total number of steps. The error of the estimate is calculated against the output of Mathematica's built-in function NIntegrate.

• middle row of graphs: Richardson extrapolation is applied twice to combine three separate approximations with , , and steps, respectively, and the error is calculated again. Notice that the total computational effort remains the same.

• bottom graph: when the absolute relative error moves below 1, Richardson extrapolation applied twice gives a better approximation. For any linear function, for example when you select , both approximations have a zero error; in this case, the outcome for the absolute relative error is 1.

[less]

Contributed by: Michail Bozoudis (July 2014)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA

Snapshots

Details

Let be an approximation of the exact value of the integral of that depends on a positive step size with an error formula of the form

,

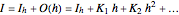where the 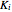are known constants. For step sizes and ,

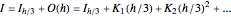
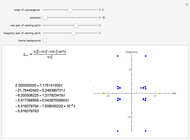
To apply Richardson extrapolation twice, multiply the last two equations by 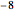and , respectively, and then, by adding all equations, the two error terms of the lowest order disappear:

.

Notice that the approximations and require the same computational effort, yet the errors are 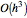and , respectively.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send