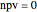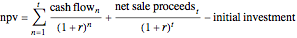Simulating the IRR

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
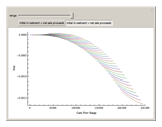
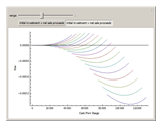
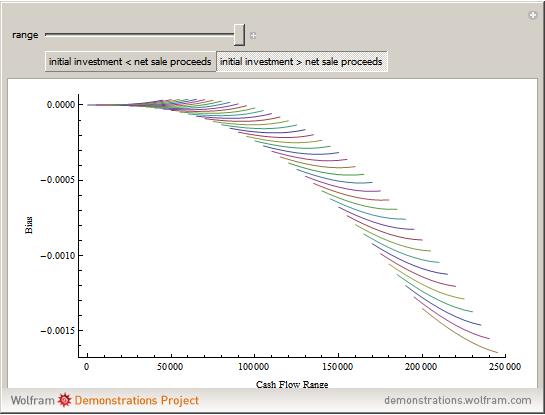
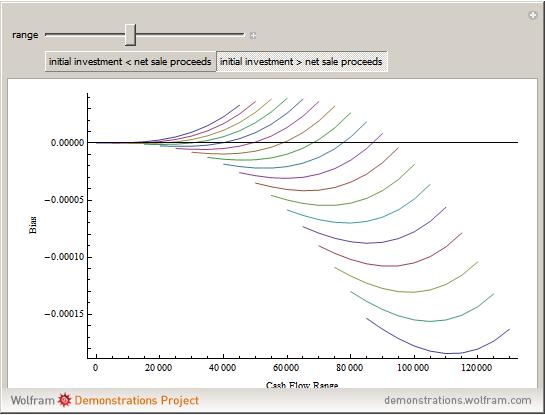
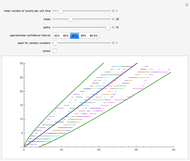
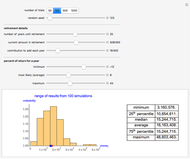
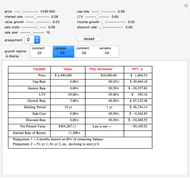
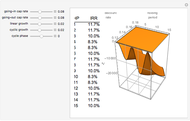
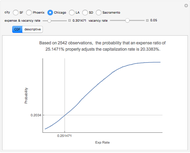
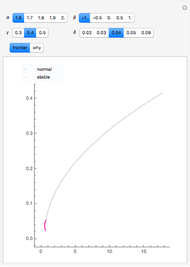
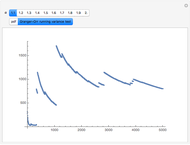
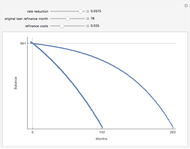
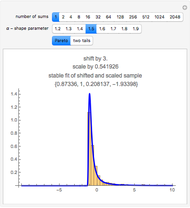
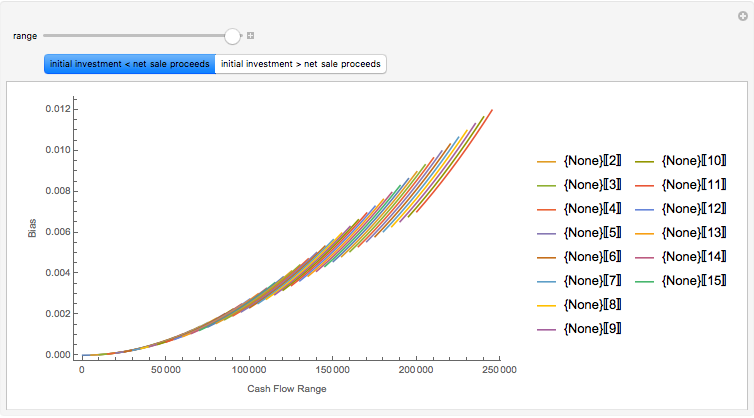
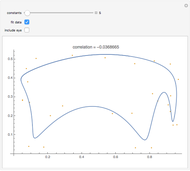
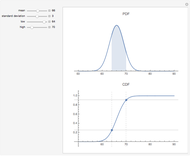
Monte Carlo simulation is useful when actual data does not exist or is hard to acquire. Many simulations are conducted for the purposes of predicting the mean or forming a probability distribution. The real estate analyst, often faced with a paucity of data, is tempted to simulate the internal rate of return (IRR) for a project. However, simulation introduces inaccuracies because of Jensen's inequality. Operationally, the problem arises from the curved nature of the IRR function. Simulation uses the concept of the expectation, which is a linear operator. Calculating an expectation for a curved function is a form of linear interpolation that has a built-in error to the extent the straight line between two points does not coincide with the curve. This Demonstration refers to this error as a bias.
[more]
Contributed by: Roger J. Brown (March 2011)
Reproduced by permission of Academic Press from Private Real Estate Investment ©2005
Open content licensed under CC BY-NC-SA
Snapshots
Details
J. L. W. V. Jensen, "Sur les fonctions convexes et les inégalités entre les valeurs moyennes," Acta Math., 30, 1906 pp. 175–193.
Jensen's inequality holds that a function 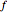 is convex in the interval
is convex in the interval 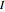 if and only if the following inequality is satisfied for all
if and only if the following inequality is satisfied for all 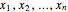 in
in 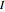 and for all
and for all 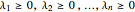 with
with 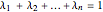 :
:  . A common description of this theorem would be that the function of the expectation is always less than or equal to the expectation of the function. The bias described in this Demonstration is a measure of how these two differ. The bias direction will depend on whether the function is convex or concave (resulting in "less than or equal to…" becoming "equal to or more than…" in the statement above).
. A common description of this theorem would be that the function of the expectation is always less than or equal to the expectation of the function. The bias described in this Demonstration is a measure of how these two differ. The bias direction will depend on whether the function is convex or concave (resulting in "less than or equal to…" becoming "equal to or more than…" in the statement above).
R. J. Brown, "Sins of the IRR," The Journal of Real Estate Portfolio Management, 12(2), 2006 pp. 195-200.
More information is available in Chapter Four of Private Real Estate Investment and at mathestate.com.
R. J. Brown, Private Real Estate Investment: Data Analysis and Decision Making, Burlington, MA: Elsevier Academic Press, 2005.
Permanent Citation