Forming the Efficient Frontier When Returns Are Non-Normal
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
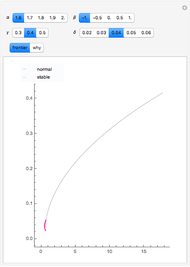
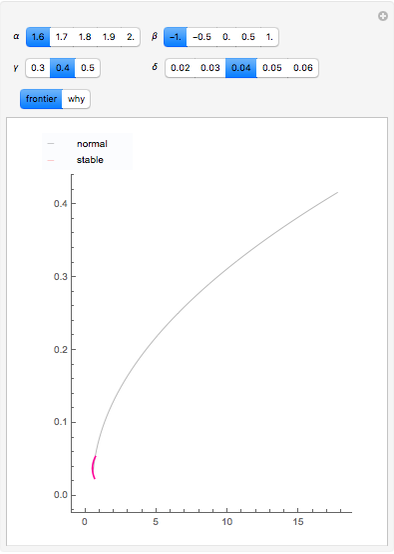
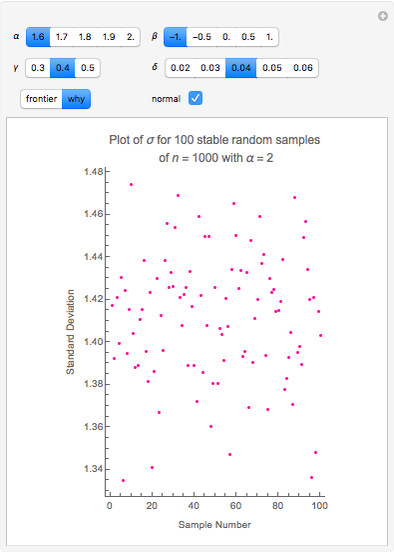
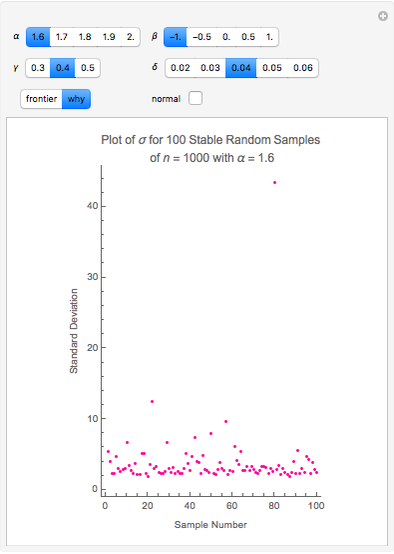
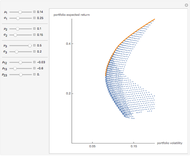
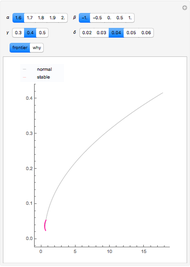
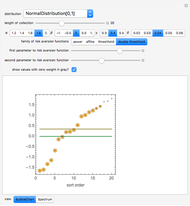
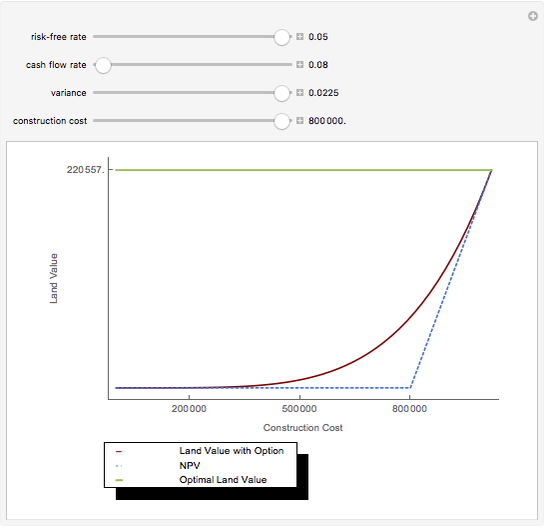
The finance paradigm since Markowitz (1952) depends heavily on the assumption that asset returns are normally distributed. If one believes that asset returns have a Lévy stable distribution or some mixture of normal and stable that exhibits heavy tails, one wonders how the so-called efficient frontier is affected. Despite the fact that, in the limit, variance does not exist for the non-normal stable distribution, one can always calculate the variance for a finite sample. This Demonstration shows how wildly erratic such a misguided effort can be. The approach is to draw three samples of stable random variates, beginning with a non-normal random draw and setting the same stable parameters {
, 
, 
, 
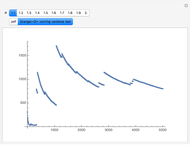
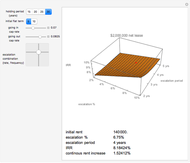
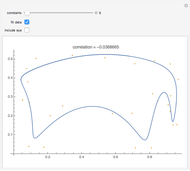
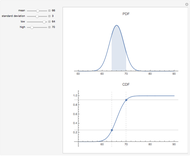
} for each within reasonably narrow bounds (to prevent the graphic from becoming too large or the axes scales becoming too small). From those samples we create the "frontier" using the conventional technology. We then take the mean and variance of the same stable sample and construct the frontier as if the sample was distributed normally and plot its "frontier". This latter, while apparently a useless exercise, is in fact what is being done by risk managers who constrain their calculations to assume normality when in fact the data are not normal. Which is the "efficient" frontier? Repeated trials show a wide variety of "frontiers" in which the normal and stable switch order, first one and then the other appearing to the left (less risky) and size (at times one or the other may appear as small as a single point). Clearly, not much can be learned about efficient asset allocation to minimize risk under these circumstances.
Contributed by: Roger J. Brown (July 2009)
Reproduced by permission of Academic Press from Private Real Estate Investment ©2005
Open content licensed under CC BY-NC-SA
Snapshots
Details
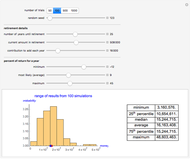
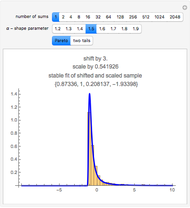
This Demonstration illustrates the widely known fact that extreme values have a disproportionate effect on the mean. Modern Portfolio Theory (MPT) and its progeny, the Capital Asset Pricing Model (CAPM) are basically static, linear models that rely on regression, a tool for predicting the mean. Distributions based on stable laws involve four parameters, three of which may be employed to model risk. Conventional models are two-parameter models, one of which is the risk parameter. Increasing the number of risk parameters in the model improves risk modeling.
This example uses the classic textbook three-asset portfolio. As a practical matter and consistent with the Capital Asset Pricing Model, more than three assets would be employed in the portfolio. As the asset count increases, the normal and stable (where 
) normal plots should become more similar but still uninformative.
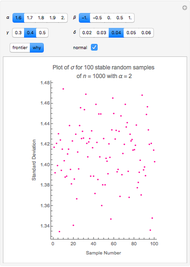
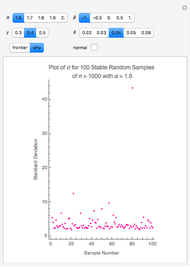
In the limit, the variance for stable, non-normal, distributions does not exist. Much of the reason for wide variation between the standard deviations for the normal and the stable, non-normal (
) cases is that standard deviation in the latter does not converge as 
grows without bounds. One encounters a sort of "chicken-and-egg" problem in making this point. Does one start with the simple theoretical fact that, in the limit, no variance means no covariance, which means no Efficient Frontier, no MPT, and no CAPM? Or does one illustrate the folly of assuming normality using finite samples that are purposely non-normal, but for which variance can still be calculated? The solution is to recognize that, while the simple equations used in 1952 to prove mathematically that diversification is a good idea may be insufficient, diversification is still a good idea. Better risk measurement at the margins emerges when modern computing technology permitting numerical solutions enlarges upon a paradigm that was developed with a #2 lead pencil using closed-form solutions.
More information is available in chapter six of Private Real Estate Investment and at mathestate.com.
More information is available in chapter six of [1] and at mathestate.com.
Reference
[1] R. J. Brown, Private Real Estate Investment: Data Analysis and Decision Making, Burlington, MA: Elsevier Academic Press, 2005.
Permanent Citation
Monte Carlo Simulation of Retirement Savings with Variable Annual Return
Paul Savory (University of Nebraska-Lincoln)
Three-Asset Efficient Frontier
Fiona Maclachlan
Efficient Single Limit Liability Insurance
Seth J. Chandler
The Efficient Dual-Limit Liability Insurance Contract
Seth J. Chandler
Expected Returns of the Dow Industrials, Beta Model
Jeff Hamrick and Jason Cawley
Expected Returns of the Dow Industrials, Fama-French Model
Jeff Hamrick and Jason Cawley
Modeling Return Distributions
Jeff Hamrick
The Effect of Holding Period on Real Estate Investment Return
Roger J. Brown
Risk, Ownership, and Control
Roger J. Brown
Stock Market Returns by Party
Theodore Gray
-
Dissolving Partnerships
Roger J. Brown -
Forming the Efficient Frontier When Returns Are Non-Normal
Roger J. Brown -
Spectral Measures
Roger J. Brown -
Granger-Orr Running Variance Test
Roger J. Brown -
Capitalization Rate Probability
Roger J. Brown -
Net Lease Economics
Roger J. Brown -
The Refinance Decision
Roger J. Brown -
True Cost of Variable Rate Mortgage Funds
Roger J. Brown -
Term Structure of Interest Rates
Roger J. Brown -
Generalized Central Limit Theorem
Roger J. Brown -
Inflation-Adjusted Yield
Roger J. Brown -
Simulating the IRR
Roger J. Brown -
Real Options
Roger J. Brown -
The Price-Terms Tradeoff
Roger J. Brown -
Fitting an Elephant
Roger J. Brown -
Solving the Subprime Loan Problem
Roger J. Brown -
Why Location Matters: The Bid Rent Curve
Roger J. Brown -
Explaining Real Estate Price Bubbles
Roger J. Brown -
Value Added Growth Model
Roger J. Brown -
Connecting the CDF and the PDF
Roger J. Brown