Terminal Velocity of Falling Particles
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
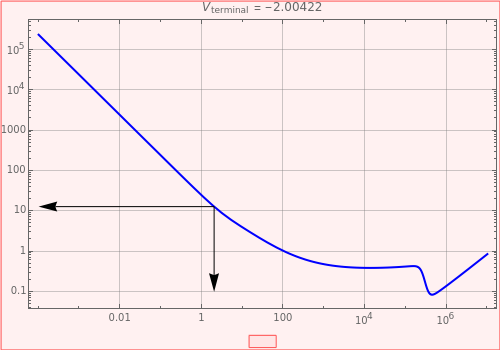
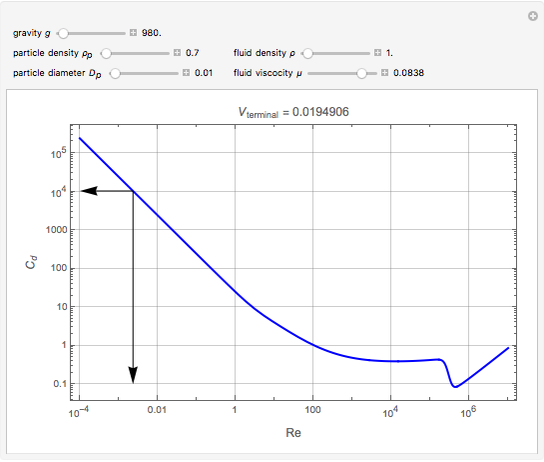
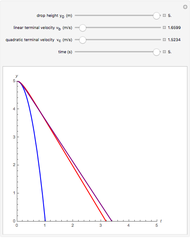
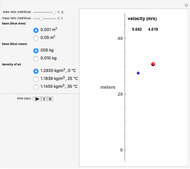
This Demonstration calculates the terminal velocity of a spherical solid particle falling in a fluid under the force of gravity.
[more]
Contributed by: Clay Gruesbeck (June 2015)
Open content licensed under CC BY-NC-SA
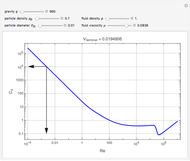
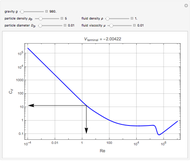
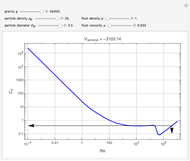
Snapshots
Details
Reference
[1] F. A. Morrison, “Data Correlation for Drag Coefficient for Sphere,” Department of Chemical Engineering, Michigan Technological University, 2013. http://www.chem.mtu.edu/~fmorriso/DataCorrelationForSphereDrag2013.pdf.
Permanent Citation