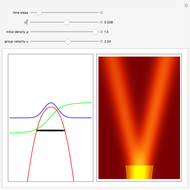
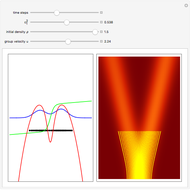
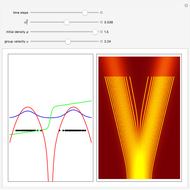
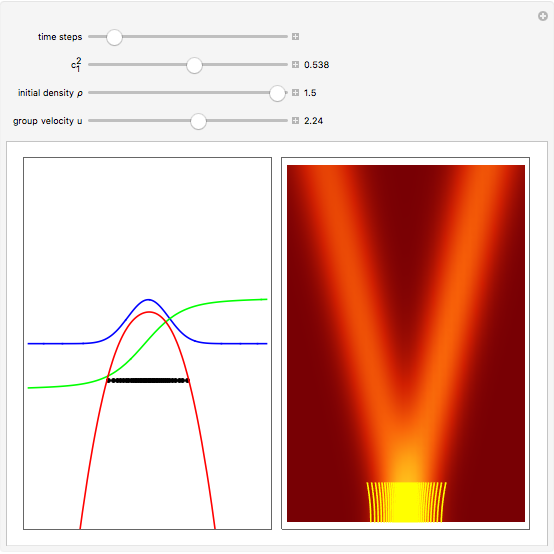
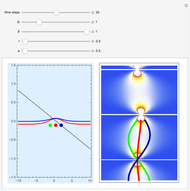
The Stern–Gerlach experiment (carried out in 1922 with silver atoms) discovered the space quantization of particles with spin. This entails a correlation between the angular momentum of a quantum particle and its trajectory in an inhomogeneous magnetic field. The particle receives an impulse from a magnetic field gradient along the axis. By measuring the position of spin 1/2 particles at a detector screen, two discrete lines are observed, rather than a single continuous trace that would be expected according to classical mechanics. In the orthodox approach to quantum mechanics, spin is an intrinsic addition to angular momentum, not necessarily associated with some well-defined motion of a material body [1]. The definite measurement of the position of the spin 1/2 particle with magnitude in a given direction leads to an uncertainty in its values in the two mutually perpendicular directions, since the corresponding spin operators do not commute. In the causal interpretation (de Broglie–Bohm interpretation) the spinor wave represents a real physical field propagating in Euclidean space (for a one-body quantum system) that imparts well-defined trajectories to quantum particles. The two lines on the screen obtained by the Stern–Gerlach measurement are the result of the alternative possible trajectories. The equation that describes the spinor wavefunction after the particle has left the inhomogeneous magnetic field is the free Pauli equation in the 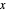direction: [2], here with . The wavefunction is a two-component spinor, with and . Each component evolves independently and has the Gaussian form for the initial packet, with initial spatial half-width and group velocity . For there is no spatial separation. The total wavefunction for the spin quantum system could be expressed by a superposition .