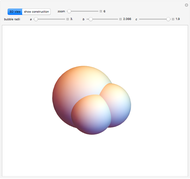
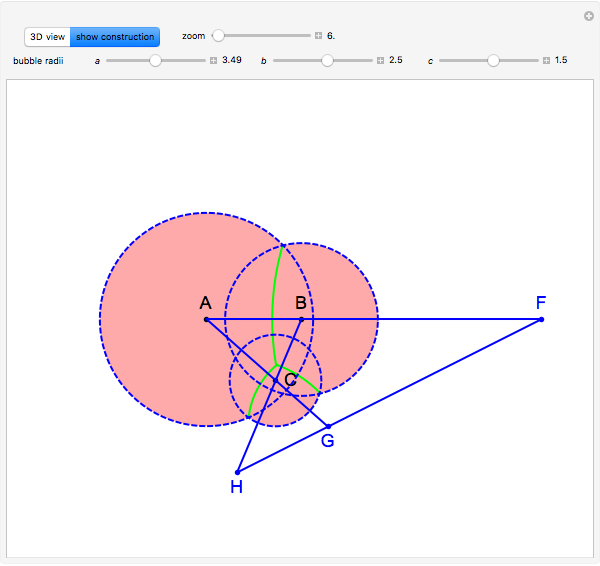
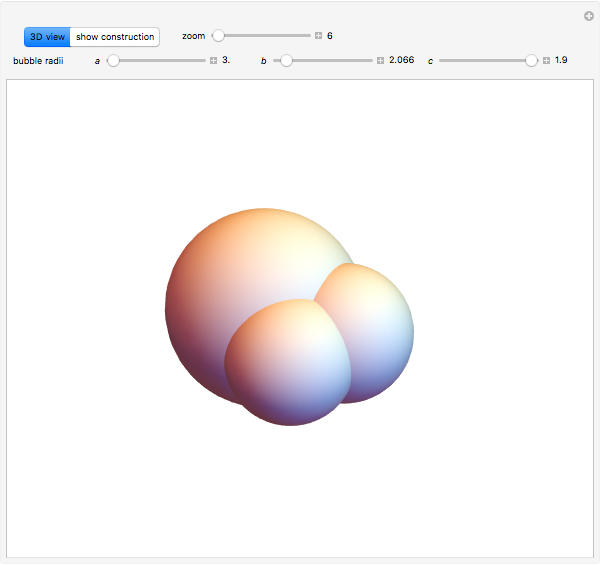
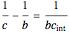Three Coalescing Soap Bubbles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
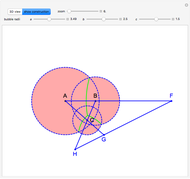
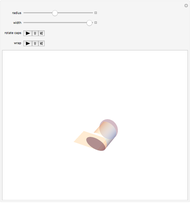
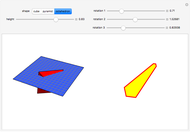
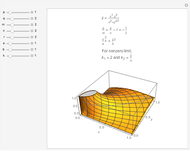
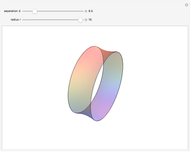
Using the calculus of variations, the Belgian mathematician Joseph Plateau deduced that the interfaces between adhering soap films represent localized minimal surfaces, which occupy minimum areas around a set of constrained geometric regions. Of course, this is not a global minimum, which would consist of a single spherical bubble. This Demonstration considers the case of three connected bubbles with variable radii, centered at 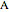 ,
,  , and
, and  . You can also choose to see the details of Plateau's construction.
. You can also choose to see the details of Plateau's construction.
Contributed by: S. M. Blinder (September 2013)
After work by: Enrique Zeleny
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] C. V. Boys, "Soap-Bubbles and the Forces Which Mould Them," London: Society for Promoting Christian Knowledge, 1896. www.gutenberg.org/files/33370/33370-h/33370-h.htm.
Permanent Citation