Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Two Coalescing Soap Bubbles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

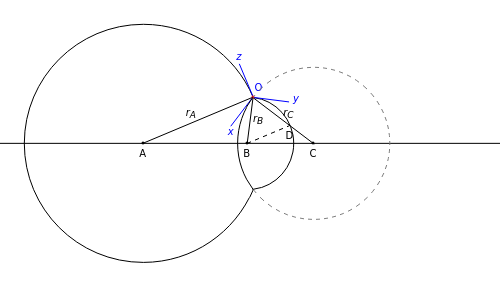
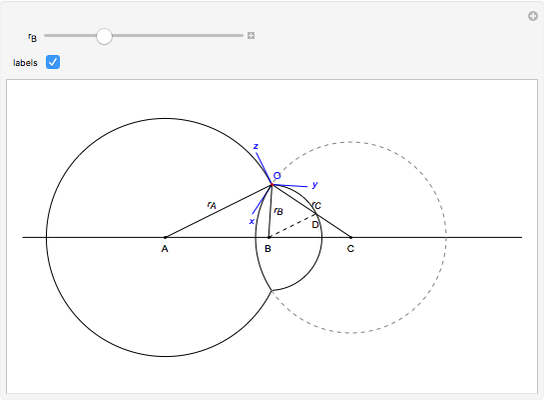
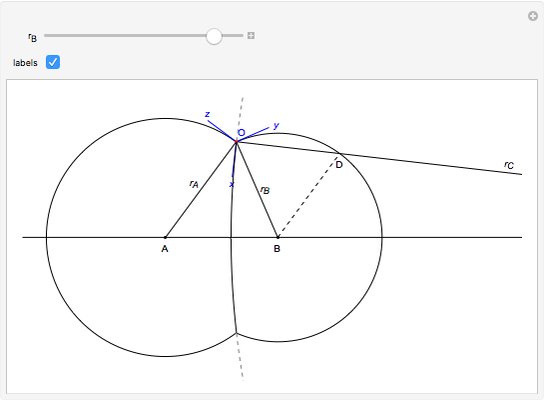
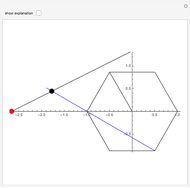
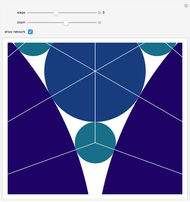
The figure shows the geometrical properties of a pair of coalescing bubbles, first studied by the Belgian physicist Joseph A. Plateau in the 1830s. The bubbles reach this configuration because the internal pressures are in equilibrium. Soap bubbles are superb examples of minimal surfaces, an important subject in mathematics.

Contributed by: Enrique Zeleny (April 2010)
Open content licensed under CC BY-NC-SA

Snapshots

Details

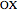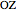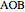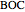The angles between the lines , , and are equal to 120°; the angles and are equal to 60°; and are right angles. The following relation holds for the radii of the three circles:

,

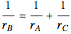where the auxiliary circle centered at C gives the curvature of the surface that separates the bubbles.

For amazing facts about bubbles, see the Ian Stewart article "Double Bubble, Toil and Trouble", and for a derivation of the relationships, see C. Isenberg, The Science of Soap Films and Soap Bubbles, New York: Dover, 1992.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send