Lévy Measures

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The structure of jumps of a Lévy process is determined by its Lévy (or characteristic) measure. For an  -dimensional Lévy process, the Lévy measure of
-dimensional Lévy process, the Lévy measure of 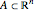 is given by the expected number, per unit time, of jumps whose size belongs to
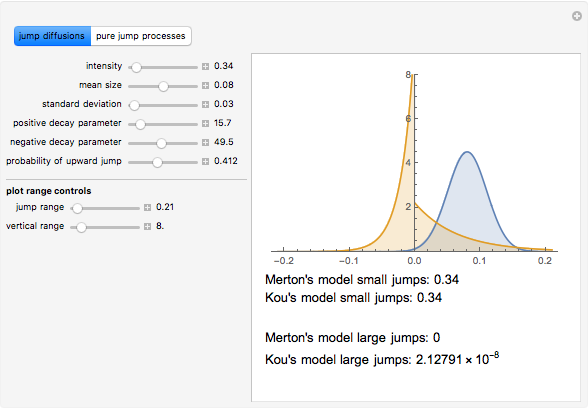
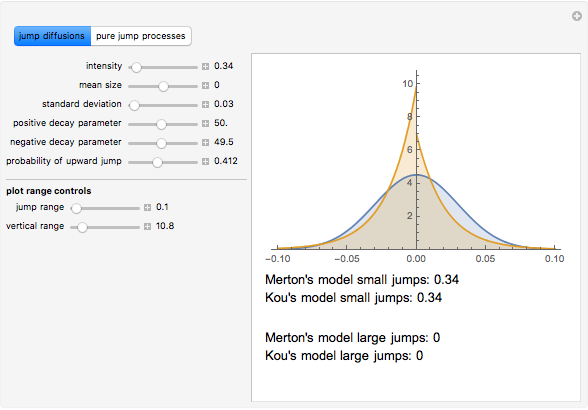
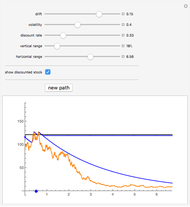
is given by the expected number, per unit time, of jumps whose size belongs to 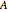 . This Demonstration compares the Lévy measures of some well-known stochastic processes that have been much used in mathematical finance. They have been divided into two groups: the jump diffusion group, consisting of the Merton and Kou models, and the pure jump processes group, consisting of the Variance Gamma and Normal Inverse Gaussian (NIG) models. The model parametrizations have been chosen to make the comparisons easier. Below the graphs of the densities of the Lévy measures, the total weights of the "small" and "large" jumps are displayed (see the Details section for further explanation). Place the mouse over the graph of a density function to see its name.
. This Demonstration compares the Lévy measures of some well-known stochastic processes that have been much used in mathematical finance. They have been divided into two groups: the jump diffusion group, consisting of the Merton and Kou models, and the pure jump processes group, consisting of the Variance Gamma and Normal Inverse Gaussian (NIG) models. The model parametrizations have been chosen to make the comparisons easier. Below the graphs of the densities of the Lévy measures, the total weights of the "small" and "large" jumps are displayed (see the Details section for further explanation). Place the mouse over the graph of a density function to see its name.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
An  -dimensional Lévy process
-dimensional Lévy process 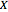 is a stochastic process with time-homogeneous independent increments, such that the sample paths of
is a stochastic process with time-homogeneous independent increments, such that the sample paths of 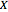 are left-continuous with right limits (almost surely), and such that
are left-continuous with right limits (almost surely), and such that  . By the Lévy-Khinchin theorem, Lévy processes are in a one-to-one correspondence with Lévy triples
. By the Lévy-Khinchin theorem, Lévy processes are in a one-to-one correspondence with Lévy triples 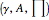 , where
, where  is a vector,
is a vector, 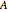 is a positive definite matrix, and
is a positive definite matrix, and  is a positive measure on
is a positive measure on 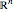 . The matrix
. The matrix 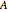 is the volatility matrix of the Brownian motion component of the Lévy process, the Lévy measure
is the volatility matrix of the Brownian motion component of the Lévy process, the Lévy measure  determines the jump structure of the process, and the vector
determines the jump structure of the process, and the vector  , sometimes called the "drift", depends on the choice of truncation function and is not an intrinsic parameter. In this Demonstration we concentrate on the Lévy measure of several well-known one-dimensional Lévy processes. The "jump diffusion" processes have nonzero Brownian component (
, sometimes called the "drift", depends on the choice of truncation function and is not an intrinsic parameter. In this Demonstration we concentrate on the Lévy measure of several well-known one-dimensional Lévy processes. The "jump diffusion" processes have nonzero Brownian component (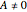 ), while the pure jump processes have no Brownian component (
), while the pure jump processes have no Brownian component (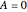 ).
).
For a fixed 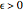 , you can consider jumps of absolute size less than
, you can consider jumps of absolute size less than  as "small jumps" and those of size larger than
as "small jumps" and those of size larger than  as "large jumps". In this Demonstration, as in [1] and [6], we take
as "large jumps". In this Demonstration, as in [1] and [6], we take  . The "total mass" of jumps of a Lévy process is given by
. The "total mass" of jumps of a Lévy process is given by 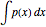 (where
(where 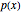 is the density of
is the density of  ) and may be finite or infinite (it is finite for the jump diffusion processes presented here and infinite for the ones that are pure jump) but the quantities
) and may be finite or infinite (it is finite for the jump diffusion processes presented here and infinite for the ones that are pure jump) but the quantities 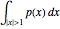 and
and 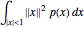 are always finite. Thus to compare large jumps of two processes we can always use their mass, that is, the value of
are always finite. Thus to compare large jumps of two processes we can always use their mass, that is, the value of 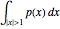 , which we display under the graphs in this Demonstration. However, to compare small jumps, we use the mass
, which we display under the graphs in this Demonstration. However, to compare small jumps, we use the mass 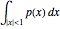 when it is finite (jump diffusions in this Demonstration) and
when it is finite (jump diffusions in this Demonstration) and 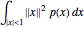 when the mass is infinite (the pure jump cases in this Demonstration). Note also that the Lévy measures of the Variance Gamma and the NIG process have a singularity at 0. The Lévy measure is not a probability measure. In fact, when the measure is finite (e.g., for jump diffusions), the total mass (i.e., the sum of the masses of small and large jumps) is equal to the jump density.
when the mass is infinite (the pure jump cases in this Demonstration). Note also that the Lévy measures of the Variance Gamma and the NIG process have a singularity at 0. The Lévy measure is not a probability measure. In fact, when the measure is finite (e.g., for jump diffusions), the total mass (i.e., the sum of the masses of small and large jumps) is equal to the jump density.
[1] R. Cont and P. Tankov, Financial Modelling with Jump Processes, Boca Raton: CRC Press, 2004.
[2] O. E. Barndorff–Nielsen, "Normal Inverse Gaussian Distributions and Stochastic Volatility Modelling," Scandinavian Journal of Statistics 24(1), 1997 pp. 1–13.
[3] S. Kou, "A Jump-Diffusion Model for Option Pricing," Management Science 48(8), 2002 pp. 1086–1101.
[4] D. B. Madan and E. Seneta, "The Variance Gamma Process (V.G.) Model for Share Market Returns," Journal of Business 63(4), pp. 511–524.
[5] R. Merton, "Option Pricing When Underlying Stock Returns Are Discontinuous," J. Financial Economics 3, 1976 pp. 125–144.
[6]. J. Bertoin, Lévy Processes, Cambridge, UK: Cambridge University Press: 1996.
Permanent Citation