Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Karhunen-Loeve Directions and Regression

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

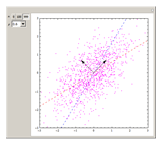
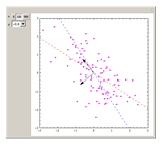
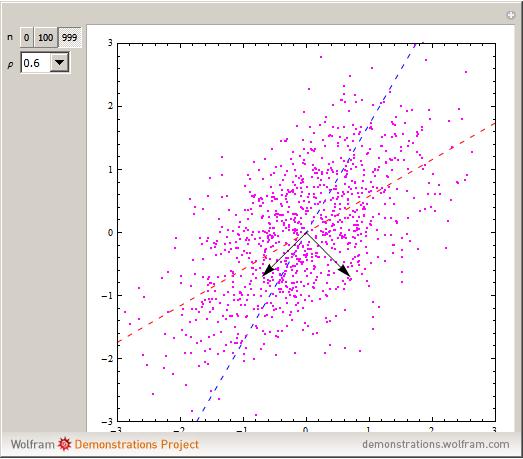
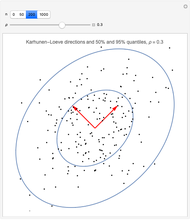
Students sometimes ask about the difference between the regression line and the Karhunen–Loeve direction. The obvious answer a professor might give is that they are different animals! The object of this Demonstration is to give a more interesting answer.

[more]

The case of variables, and , is shown. It is assumed that and are bivariate normal with means zero, variances one, and covariance . For , the expected values for the regression lines on and on are shown together with the theoretical Karhunen–Loeve directions. For the estimated regressions and directions are shown along with a scatter plot of the data.

[less]

Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Consider the multivariate random variable 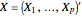with mean 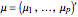and covariance matrix 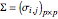. Then the Karhunen–Loeve directions are determined by columns of in the eigendecomposition 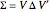, while the regression of 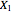on is

,

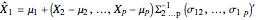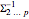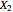where is the matrix with the first row and column removed. In the present example, this simplifies to and similarly for the regression of on .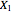

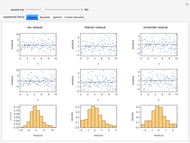
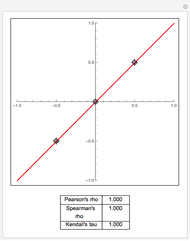
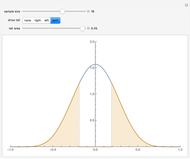
The related question based on data may be asked. In this case we just replace expectations by their sample estimates.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send