Beats Working

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
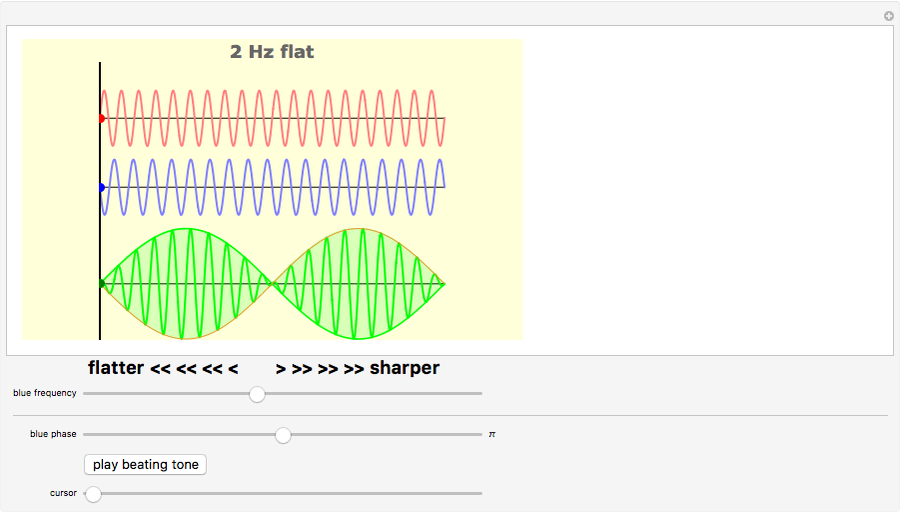
Musicians take advantage of a phenomenon called beating when they tune their instruments to a reference pitch. If two tones are very close in pitch—but not exactly the same—their combination has a pulsating or beating quality. The rate of the beating is exactly the difference between the two frequencies. Getting in tune, for the musician, is just a simple matter of getting rid of the beats.
[more]
Contributed by: John Kiehl (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
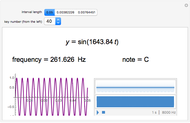
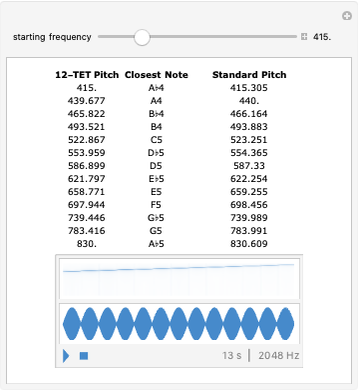
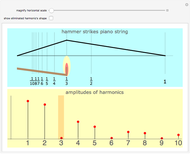
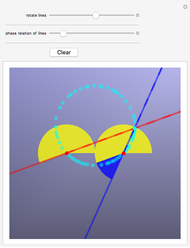
Caption 1: Frequencies are measured in Hertz (cycles per second). Here, the red and blue tones differ by 2 Hertz, so we hear a pulse every 1/2 second. Since the playback duration is preset to 3 seconds you should hear 6 beats.
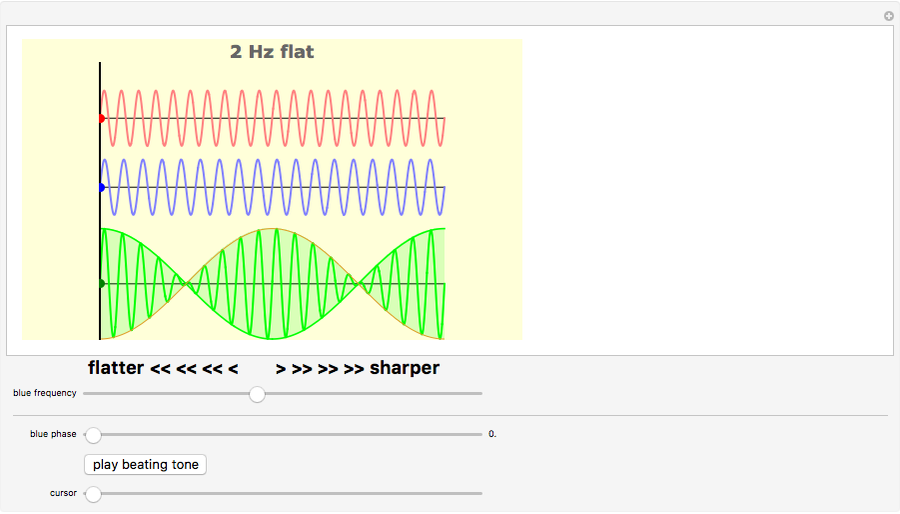
Caption 2: Varying the phase relationship between the two tones varies the phase of the beating but does not change its rate. We still hear a pulse every 1/2 second.
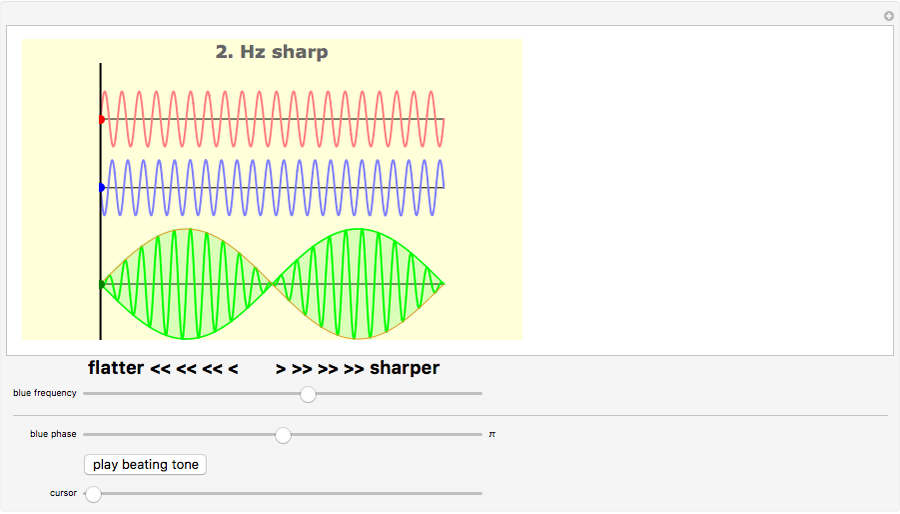
Caption 3: If the blue tone is 2 Hz sharp instead of 2 Hz flat we hear the same 2-beats-per-second pulsation.
Caption 4: Here we are out of tune by just 1/3 of a Hertz. The duration of playback is 10 seconds and we count 3 beats.
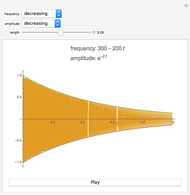
Caption 5: At greater than about a 15 Hz difference, the quality of the beating disappears and we start to hear two distinct pitches.
The trigonometric identity that is relevant to beating is the sum of two sine waves. Let  be the reference tone and
be the reference tone and  be the second tone:
be the second tone:

The right-hand side is simply the average of the two frequencies—which gets closer and closer to the desired reference frequency—modulated by the cosine of one-half the difference between the two frequencies. Since there are two peaks in one cycle of this modulating cosine wave, the number of beats per second equals exactly the difference in the frequencies of the two tones.
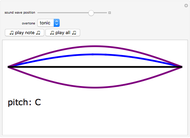
In the name of full disclosure, notice that you are listening to a 440 Hz tone, but for the sake of exposition the diagrams above are drawn with only a 20 Hz reference tone. The resulting green envelope of the beating phenomenon is, however, exactly the same for both cases.
Permanent Citation