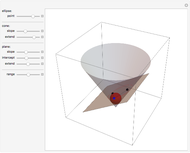
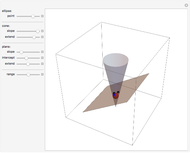
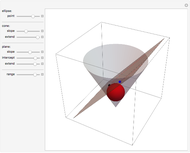
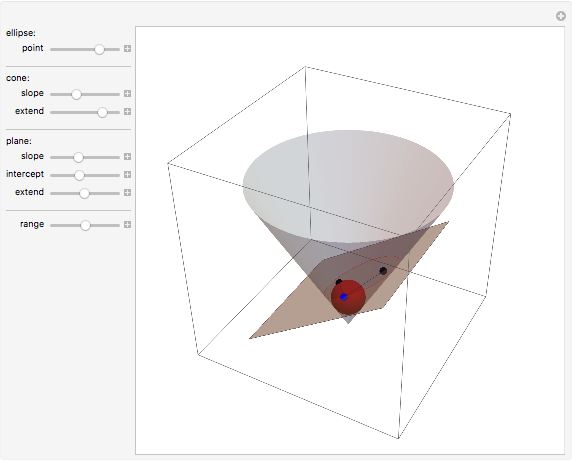
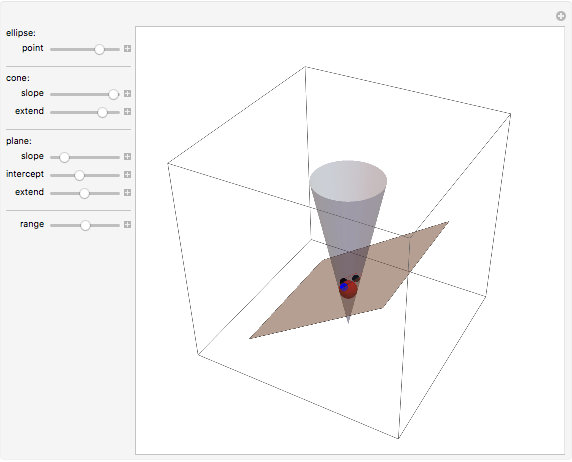
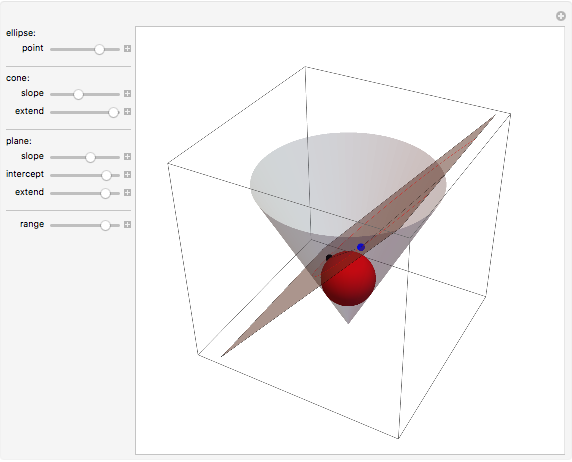
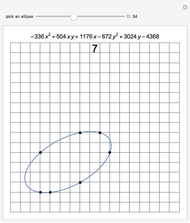
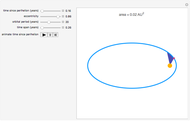
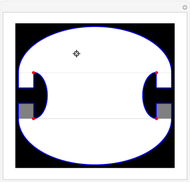
A moving droplet of blood will eventually hit a surface. At the initial instance of contact, the spherical droplet will be tangent to the intercepting surface. The type of spatter the blood droplet leaves on the surface strongly depends on its direction and speed (its vector).
In the diagram, the instance of contact is shown for the red spherical droplet. A Dandelin cone based on the vector approximates the elliptical spatter pattern the blood will leave behind. Note that the initial tangent point is one of the foci of the underlying ellipse. The speed and viscosity will further deform the elliptical pattern.
At a complex crime scene, a forensic scientist collects data on these elliptical spatter patterns, then uses trigonometry to calculate the vectors behind each spatter. The vectors lead back to a position in time for the former owner of each droplet.
Browse all topics
