Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Complex Addition of Harmonic Motions and the Phenomenon of Beats

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

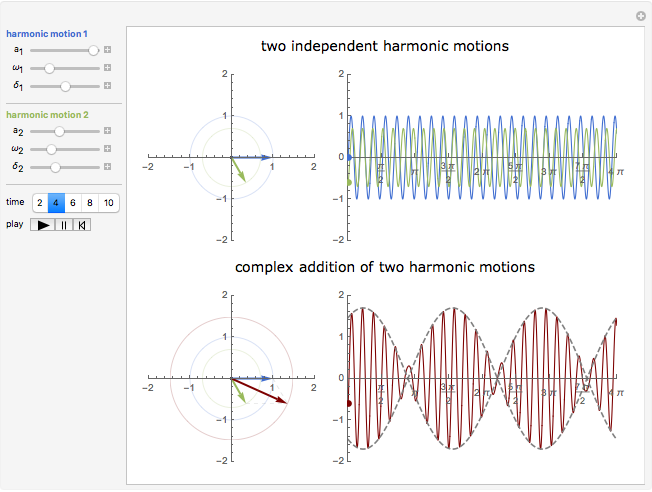
Harmonic motion can be represented by either trigonometric or complex exponential functions. Any vector 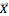in the - plane can be written as a complex number: 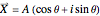, where 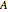is the amplitude (also called the norm) and is the phase (also called the argument). The projection onto the 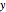axis of such a rotating vector is the imaginary part of 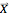. According to Euler's formula, a complex number can be expressed as 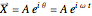, where denotes the frequency of rotation in the counterclockwise direction and is time. Multiplying by shifts the phase.

[more]

This Demonstrations shows the addition of two independent harmonic motions in terms of complex numbers. The sum of two harmonic motions with nearly equal frequencies exhibits a phenomenon known as beats.

[less]

Contributed by: Frederick Wu (October 2010)
Additional contributions by: Wei Li
Open content licensed under CC BY-NC-SA

Snapshots

Details

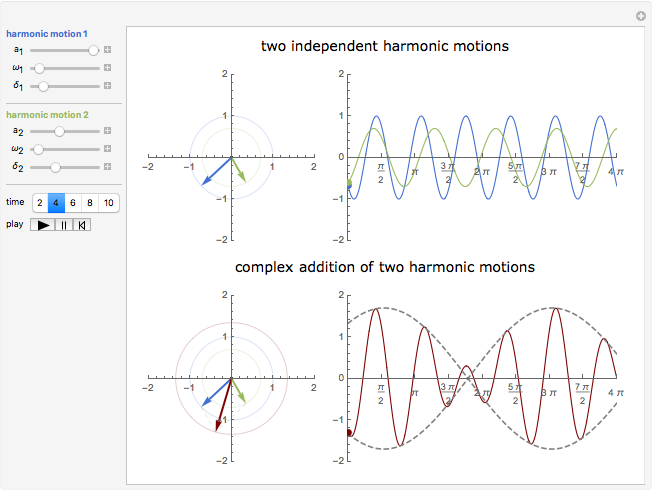
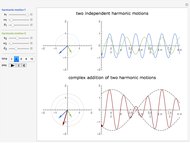
Snapshot 1: shows how two harmonic motions are added using complex numbers (left graphics) and a time series plot (right graphics)

Snapshots 2 and 3: show the beat phenomenon at different frequencies when the frequencies of the two harmonic motions are close to each other

The phenomenon of beats is often observed in machines, structures, and electric power engineering. For example, it occurs in machines when the forcing frequency is close to the natural frequency of the system.

Reference

[1] S. S. Rao, Mechanical Vibrations, 4th ed., New York: Pearson, 2004 pp. 43–53.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send