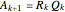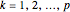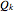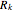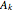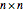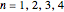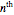Computing Eigenvalues Using the QR Algorithm

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
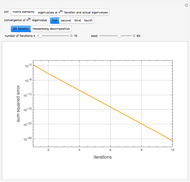
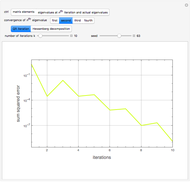
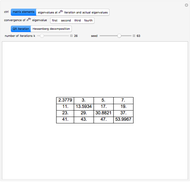
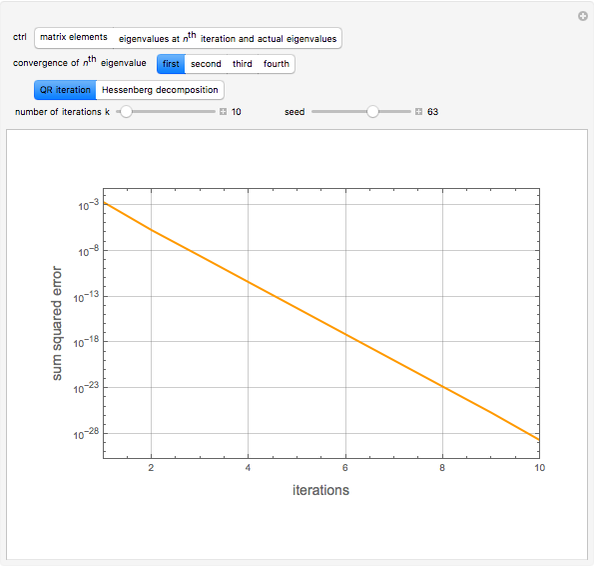
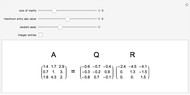
Let 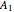 be a 4×4 matrix whose entries are the first 16 prime numbers with the main diagonal perturbed by some random noise. This Demonstration calculates the eigenvalues of
be a 4×4 matrix whose entries are the first 16 prime numbers with the main diagonal perturbed by some random noise. This Demonstration calculates the eigenvalues of 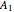 using the QR iteration method and shows the convergence properties of the iteration method.
using the QR iteration method and shows the convergence properties of the iteration method.
Contributed by: Housam Binousand Brian G. Higgins (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] K. J. Beers, Numerical Methods for Chemical Engineering, Cambridge: Cambridge University Press, 2007.
[2] G. H. Golub and C. F. Van Loan, Matrix Computations, Baltimore: Johns Hopkins University Press, 1983.
Permanent Citation