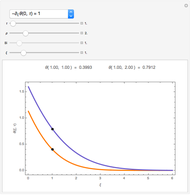
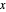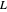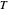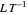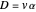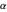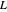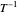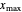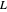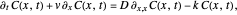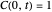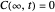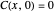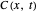Convection-Diffusion in a Semi-Infinite Region

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
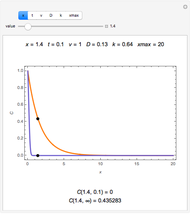
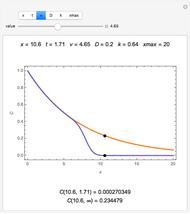
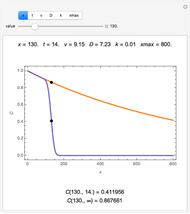
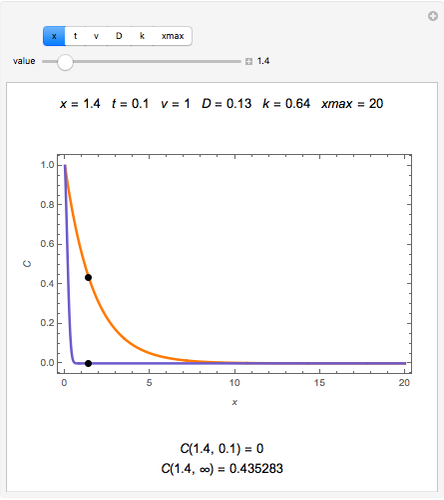
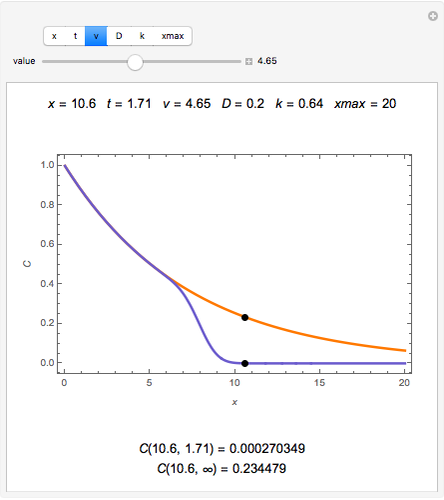
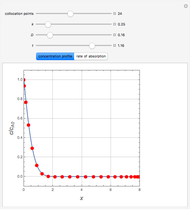
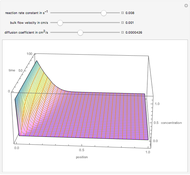
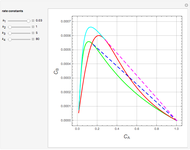
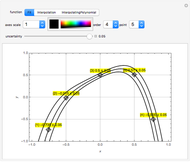
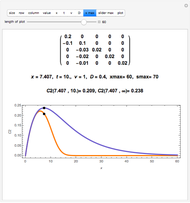
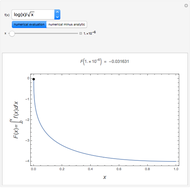
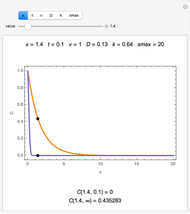
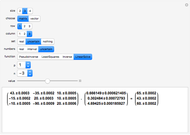
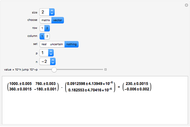
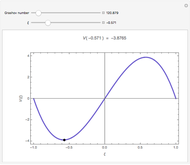
The dimensionless concentrations 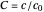 (
(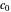 is surface concentration [
is surface concentration [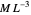 ]) in a semi-infinite region are plotted (steady state in orange, transient in blue) up to the space coordinate
]) in a semi-infinite region are plotted (steady state in orange, transient in blue) up to the space coordinate 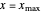 [
[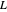 ].
].
Contributed by: Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The solution programmed includes all possible special cases. The general case is given by Bear and used to compute multispecies transport problems by Sun, et al.
J. Bear, Hydraulics of Groundwater, New York: McGraw-Hill, 1979.
Y. Sun, J. N. Petersen, T. P. Clement, and R. S. Skeen, "Development of Analytical Solutions for Multispecies Transport with Serial and Parallel Reactions," Water Resources Research, 35(1), 1999 pp. 185–190.
Permanent Citation