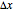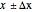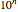Solving a Linear System with Uncertain Coefficients

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
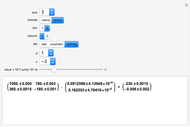
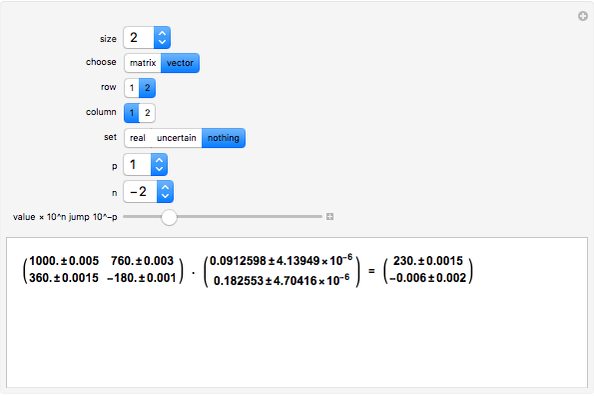
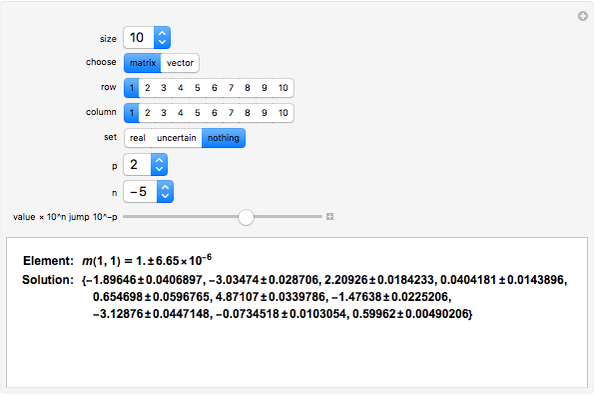
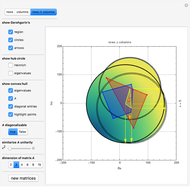
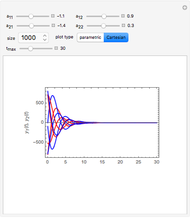
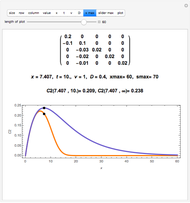
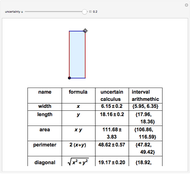
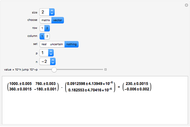
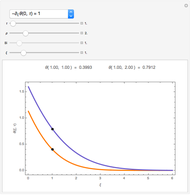
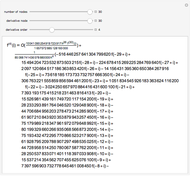
This Demonstration shows the LinearSolve solution of linear algebraic systems with uncertain numbers of the form 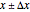 as entries. The rules are extracted from the authors' Uncertain Calculus package. The elements of the initialization diagonal matrix and right‐hand side vector are
as entries. The rules are extracted from the authors' Uncertain Calculus package. The elements of the initialization diagonal matrix and right‐hand side vector are  . The "size" of the linear system can be set from 2×2 to 10×10.
. The "size" of the linear system can be set from 2×2 to 10×10.
Contributed by: Valter Yoshihiko Aibe and Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
There is international consensus on the evaluation of standard uncertainty and combined standard uncertainty in measurement and computations [1, 2]. Just as the International System of Units (SI) has brought coherence to all scientific and technological measurements, the worldwide consensus on uncertainty permitted a vast spectrum of results to be readily understood and properly interpreted.The needs of numerous testing laboratories to calculate the measurement uncertainty in large scale are supported by numerous software tools. Rasmussen [3] reviewed 10 different software packages.
To facilitate the calculation of the combined standard uncertainty, similar to the complex and interval numbers, Aibe and Mikhailov introduced a new object, 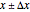 , called an uncertain number [4] and implemented the Uncertain Calculus in Mathematica 6. It transforms a functional relationship of uncertain numbers
, called an uncertain number [4] and implemented the Uncertain Calculus in Mathematica 6. It transforms a functional relationship of uncertain numbers 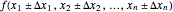 into an uncertain number
into an uncertain number 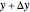 , assuming that all arguments of the function
, assuming that all arguments of the function 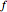 are independent. It is related to interval arithmetic. The key difference is that this model of propagating uncertainty, under the standard arithmetic operations of plus, times, and power, is more realistic than the worst-case assumption underlying interval arithmetic's propagation of independent error. Specifically, an
are independent. It is related to interval arithmetic. The key difference is that this model of propagating uncertainty, under the standard arithmetic operations of plus, times, and power, is more realistic than the worst-case assumption underlying interval arithmetic's propagation of independent error. Specifically, an  model of propagation is used, rather than the more conservative
model of propagation is used, rather than the more conservative 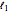 model of interval operations.
model of interval operations.
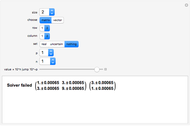
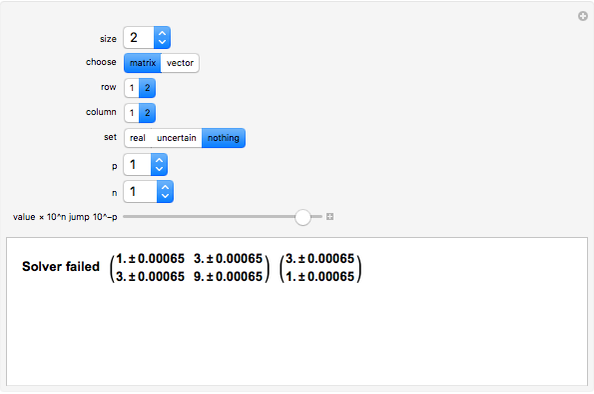
It is important to realize that uncertainty propagation, like error propagation from interval arithmetic, is defined operationally. This means, among other things, that a "black box" solver, such as the LinearSolve function of Mathematica, can give different results when using different methods. In particular, results will be heavily influenced by the internal pivot selection strategy. They will also be affected, though to a lesser extent, by whether row reduction is done in two separate stages (forward, then reverse), versus clearing both below and above pivots at the same time.
References:
1. European Cooperation for Accreditation of Laboratories, Expression of the Uncertainty of Measurement in Calibration, EAL-R2 and EAL-R2-S1, 1997.
2. International Organization for Standardization, Guide to the Expression of Uncertainty in Measurement, Geneva, Switzerland, 1993.
3. S. N. Rasmussen, "Software Tools for the Expression of Uncertainty in Measurement," MetroTrade Workshop on Traceability and Measurement Uncertainty in Testing, Berlin, January 30–31, 2003.
4. V. Y. Aibe and M. D. Mikhailov, "Uncertainty Calculus in Metrology," Proceedings of ENCIT 2008, 12th Brazilian Congress of Thermal Engineering and Sciences, Belo Horizonte, MG, Brazil, November 10–14, 2008.
Permanent Citation