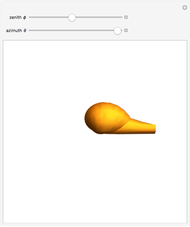
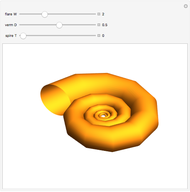
Crooked Church Spire

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
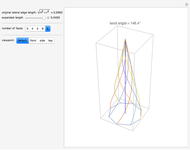
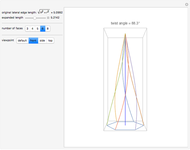
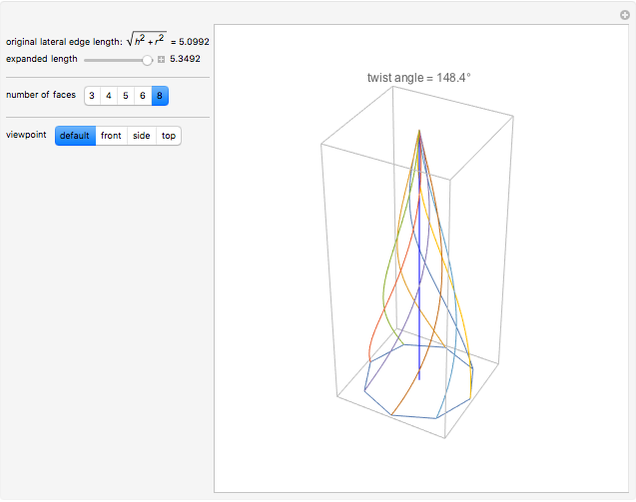
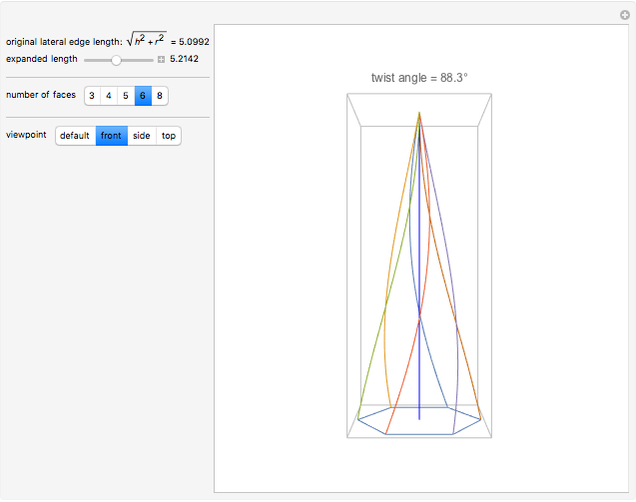
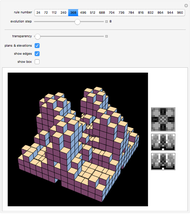
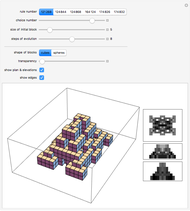
A crooked (or twisted) spire is a pyramidal tower with a twist relative to its base. This can be by design or as a result of changes over time caused by weathering [1].
[more]
Contributed by: Erik Mahieu (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The twisted lateral edges of a right pyramid have the parametric equation of a conical spiral:
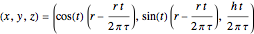 .
.
The base of the pyramid is a  -sided regular polygon (and
-sided regular polygon (and  is also is the number of lateral faces of the pyramid),
is also is the number of lateral faces of the pyramid),  is the height of the apex, and
is the height of the apex, and  (equal to
(equal to 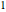 in this Demonstration) is the radius of the circle through the vertices of the base.
in this Demonstration) is the radius of the circle through the vertices of the base.
Using the built-in Mathematica function ArcLength, the length of the lateral edges can be calculated using the formula:
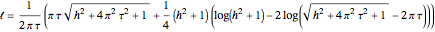 .
.
From this, one can calculate a numerical approximation of the number of twists  over
over  as a function of the arc length
as a function of the arc length  . Using regression analysis, one finds this fitted model:
. Using regression analysis, one finds this fitted model:
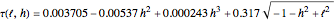 .
.
The twist angle is taken to be 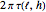 or the angle by which the pyramid is twisted relative to its base.
or the angle by which the pyramid is twisted relative to its base.
References
[1] Friends of Chesterfield Parish Church. "Notes on the Church." (Jun 9, 2015) www.friendsofthecrookedspirechesterfield.co.uk/notesonthechurch.php.
[2] Wikipedia. "Church of St Mary and All Saints, Chesterfield." (Jun 9, 2015) en.wikipedia.org/wiki/Church_of_St _Mary _and _All _Saints,_Chesterfield.
Permanent Citation