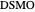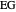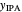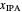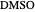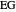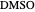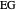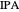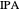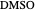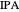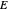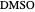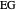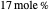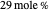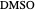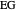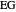Entrainer Selection for Homogeneous Azeotropic Distillation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
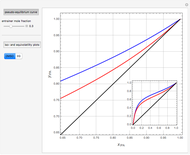
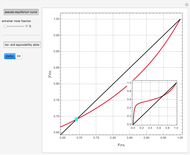
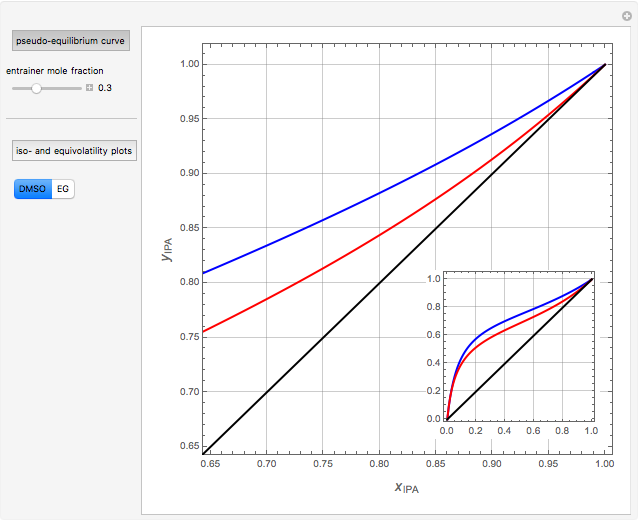
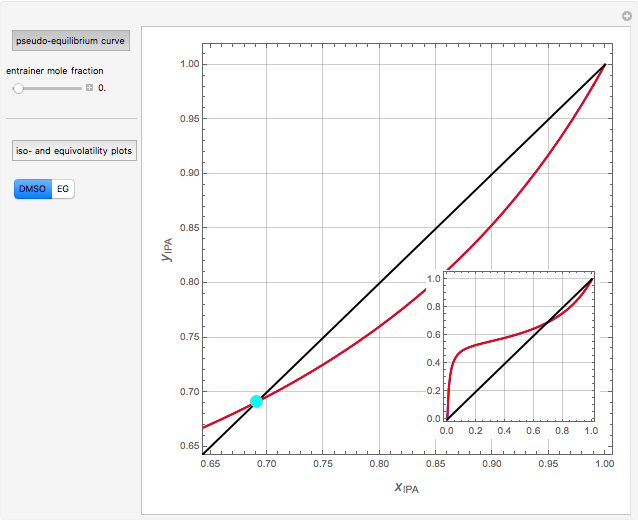
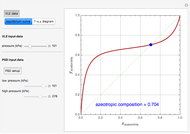
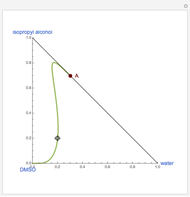
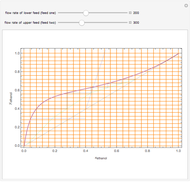
Separation of a mixture of isopropyl alcohol (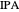 ) and water is impossible with a single distillation column because of the existence of a minimum-boiling homogeneous azeotrope (
) and water is impossible with a single distillation column because of the existence of a minimum-boiling homogeneous azeotrope (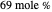
 ,
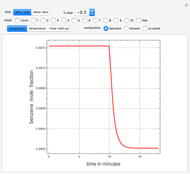
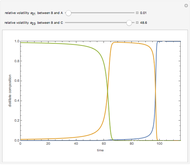
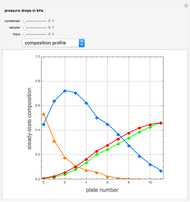
,  ). This Demonstration illustrates how the addition of an extraneous component, called an entrainer, can facilitate the separation. The entrainer alters the relative volatilities of the components and thereby "breaks" the azeotrope. Homogeneous azeotropic distillation generally uses a heavy entrainer, which does not introduce new azeotropes.
). This Demonstration illustrates how the addition of an extraneous component, called an entrainer, can facilitate the separation. The entrainer alters the relative volatilities of the components and thereby "breaks" the azeotrope. Homogeneous azeotropic distillation generally uses a heavy entrainer, which does not introduce new azeotropes.
Contributed by: Housam Binous, Naim Faqir, and Brian G. Higgins (October 2012)
Open content licensed under CC BY-NC-SA
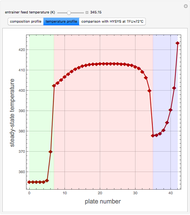
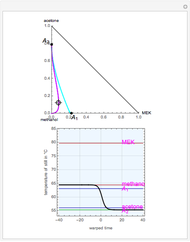
Snapshots
Details
References
[1] V. Julka, M. Chiplunkar, and L. O'Young, "Selecting Entrainers for Azeotropic Distillation," Chemical Engineering Progress, March 2009 pp. 47–53.
[2] L. Laroche, H. W. Andersen, M. Morari, and N. Bekiaris, "Homogeneous Azeotropic Distillation: Comparing Entrainers," The Canadian Journal of Chemical Engineering, 69(6), 1991 pp. 1302–1319. doi: 10.1002/cjce.5450690611.
[3] W. L. Luyben and I.-L. Chien, Design and Control of Distillation Systems for Separating Azeotropes, Hoboken, NJ: Wiley, 2010.
[4] S. Arifin and I-L. Chien, "Design and Control of an Isopropyl Alcohol Dehydration Process via Extractive Distillation Using Dimethyl Sulfoxide as an Entrainer," Industrial and Engineering Chemistry Research, 47(3), 2008 pp. 790–803. doi: 10.1021/ie070996n.
Permanent Citation