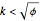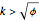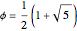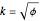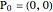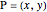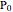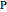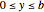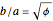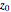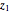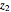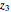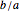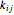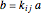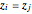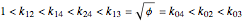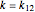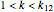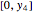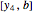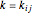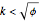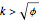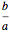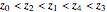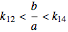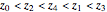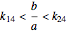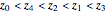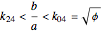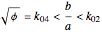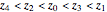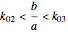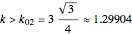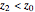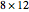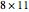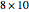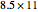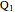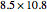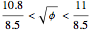Mathematica MathWorld Wolfram Science More »

HOME

TOPICS

LATEST

Exploring the Crease Length Problem

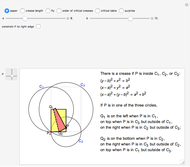
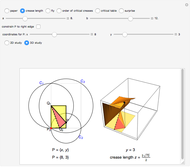
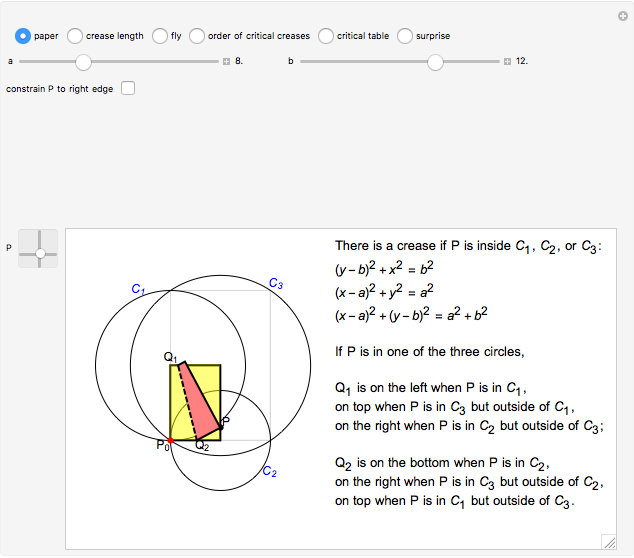
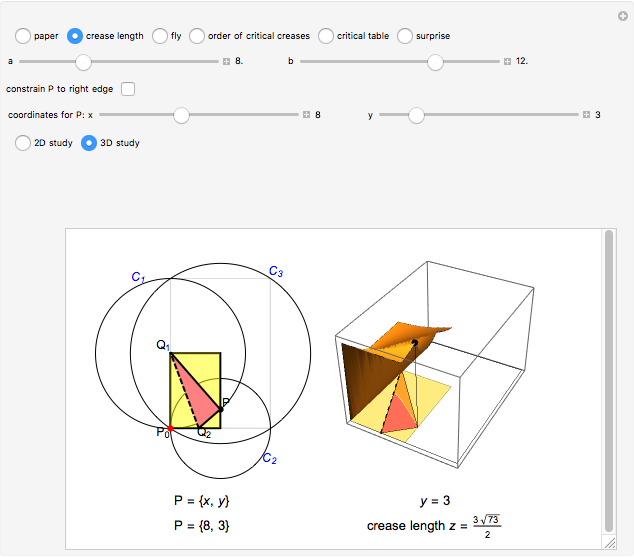
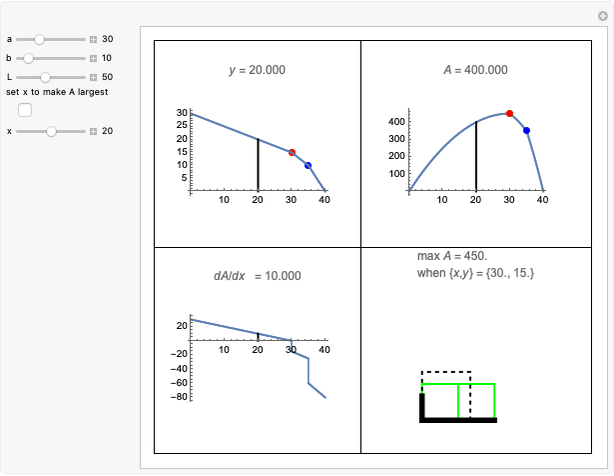
The crease length problem: Fold the lower left corner of a sheet of paper

inches wide and

inches high, with

, to the right edge and crease. What fold gives the shortest crease? The problem becomes interesting when you consider folds with "flaps", not just folds that intersect the left and bottom edges.

The "text book" solution is to fold so the lower endpoint of the crease is three quarters of the way to the right corner. When

, this crease is shortest among creases that intersect the left and bottom edges. But it is never the shortest crease.

The folds giving the shortest and longest creases depend in a remarkable way on the ratio

. When

, where

(the golden ratio), there are two distinct shortest creases and two distinct longest creases. There are other special

, when local extrema have the same value.

Choose "paper" to play with folding

or choose "crease length". Vary

and

to change the shape of the paper. The point P can be restricted to the right edge of the paper. Note how crease length along the right edge changes with

Folding

, the graph of crease length as a function of

looks like a flying bird, /\/\. There are five critical folds, with local extrema

and

. The order of these local extrema changes as

is varied.

Choose "critical table" to see formulas and select "values" to study the values of P, the crease endpoints

, and crease length

at the critical folds. Study the

numerically by varying

and

. Select

to see the values for

, when

Choose "fly" to fly the crease length graph by selecting "

" and varying

. It is interesting to set

to 8 or 8.5 and vary

. Select one of the

to see the graph when

and

. The table to the right shows the special values of

for a given

Choose "critical folds" to see critical folds in order of critical crease length. Study by varying

(with b/a selected) or by selecting one of the

. Note there are two equalities

and

when selecting

, which are both equal to

. Otherwise, the min and max crease lengths are either

and

(when

) or

and

(when

). The order of the critial folds changes at each "special k".

Another special k of interest is

. When

, z₂<z₀ and the textbook solution is "correct" when the problem is to find the shortest crease among folds that intersect the bottom edge. Examples are 8x12 (for Stewart) and 8x11 (for Gardner). But the incomplete textbook solution is not correct for 8x10 or 8.5x11 paper, because

Choose "surprise" to see how different the results can be for paper of almost the same shape.

Contributed by: Roger B. Kirchner

Show Initialization Code

(33 lines omitted)

My step-grandson William Jons, studying for an UMTYMP (University of Minnesota Talented Youth Mathematics Program) exam, asked me about problem 65 in section 4.7 of Stewart. I'm grateful to him for stirring my interest in using Mathematica to investigate the problem.

Stewart includes a figure with the crease intersecting the left and bottom edges, and adds, "In other words, how would you choose

(the distance along the bottom from the left corner) to minimize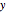

(the length of the crease)." The student is discouraged from considering folds with flaps. Gardner has a figure with a flap and the crease intersecting the top and bottom edges, but his solution ignores this case. Luckily, he used 8x11 paper and not 8x10 or 8.5x11.

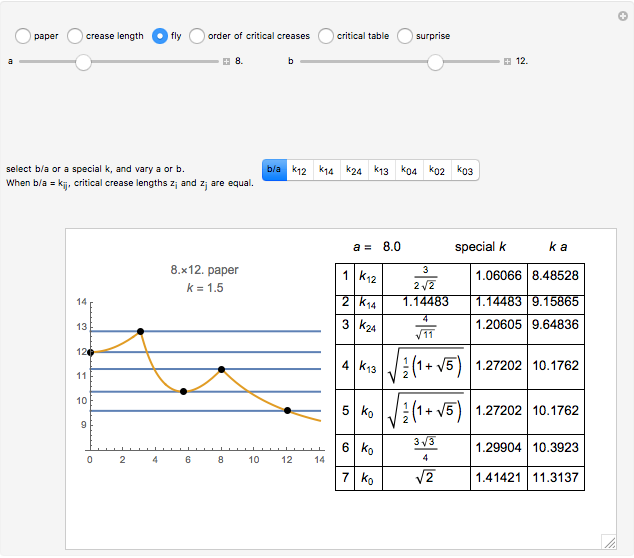
The Demonstration "Optimize the Length of the Crease of a Folded Piece of Paper" considers folds with creases that intersect the two short sides, but not creases which intersect the two long sides. This misses the opposite corner fold, which has the shortest crease for 8.5 x 11.75 paper.

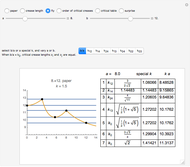
After discovering what I thought were amazing things, including a connection with the golden ratio, I found Ellermeyer had already discovered some of the same things.

References:

J. Stewart, Calculus: Early Transcendentals, 5th ed., Belmont, CA: Brooks/Cole, 2007.

M. Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, New York: Simon and Schuster, 1961.

S. Ellermeyer, "A Closer Look at the Crease Length Problem," Mathematics Magazine, 81(2), 2008 pp. 138-145.

"Exploring the Crease Length Problem" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/ExploringTheCreaseLengthProblem/

Contributed by: Roger B. Kirchner

Report an issue »

Interact with Demonstrations using the latest version of the free Mathematica Player—Download Now

Browse all topics

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

Wolfram Research

Site Index

RSS

Atom