Coconuts, Sailors, and a Monkey

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
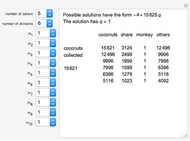
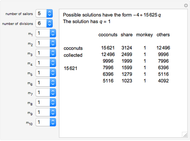
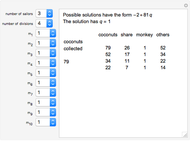
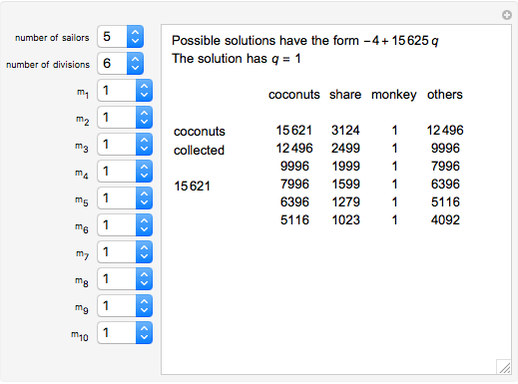
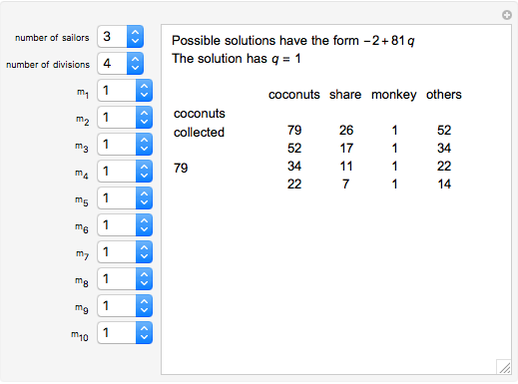
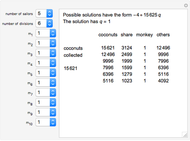
Sailors, stranded on an island, collect all the coconuts they can find. They agree to divide up the coconuts in the morning. But each, in turn, gets up in the night to take his share from the pile. At each division, one is given to a monkey to keep him quiet. In the morning, none are surprised at how the pile has shrunk. They give another coconut to the monkey and divide what remains. What is the smallest number of coconuts such that all divisions come out even?
[more]
Contributed by: Roger B. Kirchner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let there be  sailors and
sailors and  divisions. Let
divisions. Let 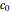 ,
, 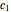 , …,
, …, 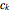 be the initial and subsequent numbers of coconuts in the pile,
be the initial and subsequent numbers of coconuts in the pile,  , ...,
, ..., 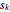 the sailors' shares, and
the sailors' shares, and 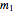 , …,
, …, 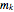 the monkey's share at the
the monkey's share at the  divisions.
divisions.
Then, 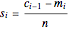 and
and 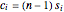 ,
, 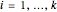 .
.
Many methods have been used to solve this problem. We recognize 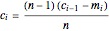 as a linear nonhomogeneous difference equation in
as a linear nonhomogeneous difference equation in 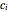 . Its solution is
. Its solution is 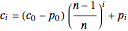 , where
, where  is a particular solution to the equation,
is a particular solution to the equation,  .
.
The difference equation can be rewritten as 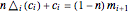 .
.
A particular solution can be verified to be 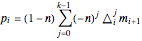 , where we define
, where we define 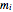 for
for 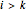 so that the
so that the 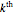 and higher differences are zero; for example,
and higher differences are zero; for example, 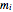 could be defined by an interpolating polynomial of degree
could be defined by an interpolating polynomial of degree  . Note that
. Note that 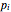 is an integer,
is an integer, 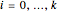 .
.
Since 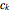 is an integer, and
is an integer, and  ,
, 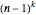 divides
divides  .
.
Therefore, 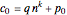 ,
, 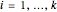 , where
, where  is the smallest integer such that
is the smallest integer such that 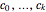 are all positive, where
are all positive, where  . The
. The 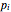 can be generated from
can be generated from 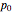 using the difference equation.
using the difference equation.
If 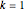 , then
, then 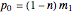 .
.
If  , then
, then 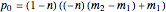 .
.
If 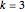 , then
, then 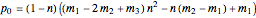 .
.
If  ,
, 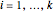 , then
, then 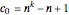 . When
. When 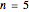 and
and 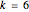 ,
,  This is the most famous case, with the monkey getting one coconut at each division.
This is the most famous case, with the monkey getting one coconut at each division.
If  ,
,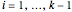 and
and  , then
, then 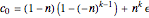 , where
, where  if
if  is even and
is even and  if
if  is odd. When
is odd. When  and
and 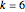 ,
,  . This is the case where the monkey does not get a coconut in the last division. See the Williams's problem below.
. This is the case where the monkey does not get a coconut in the last division. See the Williams's problem below.
How many coconuts are there if  , the monkey gets 10 coconuts at each division in the night, and none in the morning? Answer:
, the monkey gets 10 coconuts at each division in the night, and none in the morning? Answer: 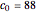 .
.
How many coconuts are there if  , the monkey removes 2 before the first division, adds 2 before the second, removes 2 before the third, and gets one in the morning?
, the monkey removes 2 before the first division, adds 2 before the second, removes 2 before the third, and gets one in the morning? 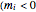 corresponds to the monkey adding to the pile.) Answer:
corresponds to the monkey adding to the pile.) Answer: 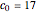 .
.
In the classical examples, 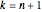 . But individual sailors could get up more than once or not at all. The monkey can take or add any number of coconuts at each division. Also, if n = 1 then k = 1, since the coconuts are gone after one "division".
. But individual sailors could get up more than once or not at all. The monkey can take or add any number of coconuts at each division. Also, if n = 1 then k = 1, since the coconuts are gone after one "division".
Suppose  ,
,  ,
,  , and
, and  . (The monkey adds 10, there is one division at night, and the monkey gets the 10 back in the morning.) In this case,
. (The monkey adds 10, there is one division at night, and the monkey gets the 10 back in the morning.) In this case,  , the possibilities are
, the possibilities are 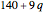 , and the minimum number of coconuts is
, and the minimum number of coconuts is 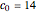 , when
, when  .
.
Martin Gardner's chapter "The Monkey and the Coconuts", in The Second Scientific American Book of Mathematical Puzzles and Diversions, begins with a problem included in a short story by Ben Ames Williams entitled "Coconuts", which appeared in the October 9, 1926 issue of The Saturday Evening Post. The magazine received over 2,000 letters the first week from readers who wanted to know, "How many coconuts?" Here is the problem as originally published:
"Five men and a monkey were shipwrecked on a desert island, and they spent the first day gathering coconuts for food. Piled them all up together and then went to sleep for the night. But when they were all asleep one man woke up, and he thought there might be a row about dividing the coconuts in the morning, so he decided to take his share. So he divided the coconuts into five piles. He had one coconut left over, and he gave that to the monkey, and he hid his pile and put the rest all back together. By and by the next man woke up and did the same thing. And he had one left over, and he gave it to the monkey. And all five of the men did the same thing, one after the other; each one taking a fifth of the coconuts in the pile when he woke up, and each one having one left over for the monkey. And in the morning they divided what coconuts were left, and they came out in five equal shares. Of course each one must have known there were coconuts missing; but each one was guilty as the others, so they didn't say anything. How many coconuts were there in the beginning?"
Williams modified an older problem in order to make it more confusing. The older problem has a coconut for the monkey at each of the six divisions, whereas in Williams' problem, the last division comes out even.
Gardner has claimed, "Today the problem of the coconuts is probably the most worked on and least-often solved of all the Diophantine brain-teasers."
The explicit formula above first appeared in "The Generalized Coconut Problem," by Roger B. Kirchner.
M. Gardner, The Second Scientific American Book of Mathematical Puzzles and Diversions, Chicago: The University of Chicago Press, 1961.
R. B. Kirchner, "The Generalized Coconut Problem," The American Mathematical Monthly, 67(6), 1960 pp. 516–519.
Permanent Citation