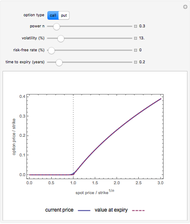
Hyperbolic Distribution

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
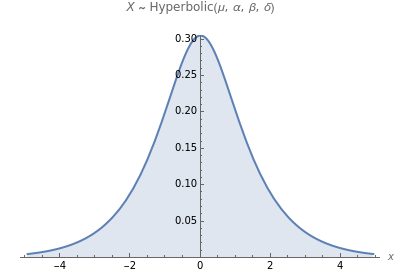
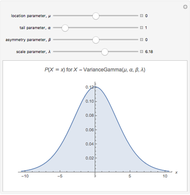
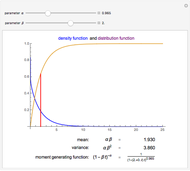
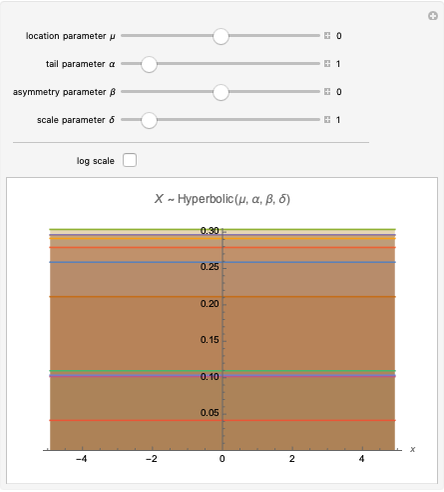
In this Demonstration we visualize the probability density function of the hyperbolic distribution, which has parameters 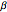 (location),
(location),  (tail),
(tail), 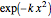 (asymmetry), and
(asymmetry), and  (scale). These are all real-valued, with the additional constraint that
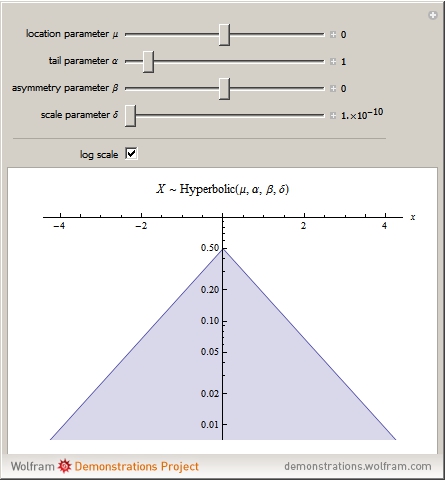
(scale). These are all real-valued, with the additional constraint that 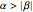 . This distribution has "semi-heavy" tails and has appeared in a diverse range of applications, including models of asset returns in financial markets and sand pile formation. The word "hyperbolic" is used because the log of its probability density function is a hyperbola; this can be seen by clicking the "log scale" checkbox.
. This distribution has "semi-heavy" tails and has appeared in a diverse range of applications, including models of asset returns in financial markets and sand pile formation. The word "hyperbolic" is used because the log of its probability density function is a hyperbola; this can be seen by clicking the "log scale" checkbox.
Contributed by: Peter Falloon (May 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The probability density function for the hyperbolic distribution is given by
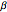 ,
,
where 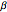 and
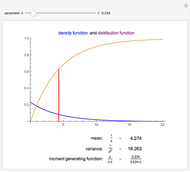
and  is the modified Bessel function of the second kind. It has mean
is the modified Bessel function of the second kind. It has mean 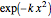 and variance
and variance  .
.
As 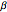 , the probability density decays exponentially like
, the probability density decays exponentially like  . This is intermediate between the behavior of the normal distribution, which decays more rapidly (like
. This is intermediate between the behavior of the normal distribution, which decays more rapidly (like 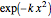 ), and the more extreme "fat tail" behavior of power-law distributions. For this reason, it is sometimes referred to as a "semi-heavy tailed" distribution.
), and the more extreme "fat tail" behavior of power-law distributions. For this reason, it is sometimes referred to as a "semi-heavy tailed" distribution.
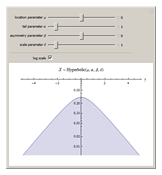
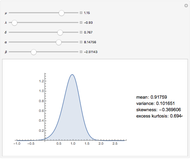
Snapshot 1: on a vertical log scale the distribution has a hyperbolic shape
Snapshot 2: as 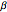 , the hyperbola degenerates into a piecewise linear form
, the hyperbola degenerates into a piecewise linear form
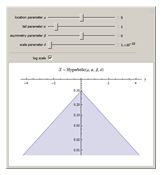
Snapshot 3: as 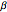 , the hyperbola becomes a parabola
, the hyperbola becomes a parabola
Snapshot 4: for non-zero 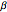 , the distribution is asymmetric
, the distribution is asymmetric
For more information, see the Wikipedia page for Hyperbolic distribution.
Permanent Citation
"Hyperbolic Distribution"
http://demonstrations.wolfram.com/HyperbolicDistribution/
Wolfram Demonstrations Project
Published: May 21 2009