Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

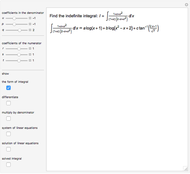
Haar Functions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

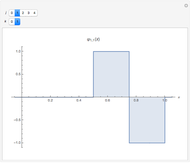
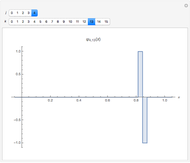
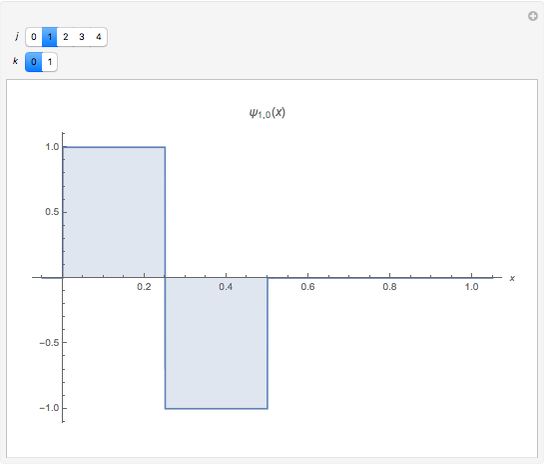
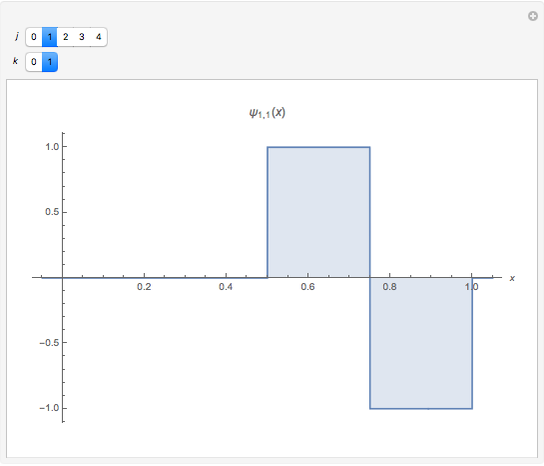
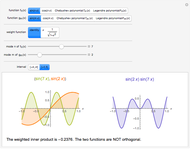
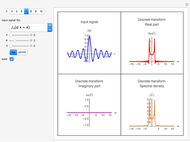
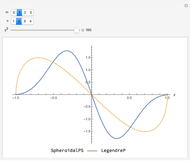
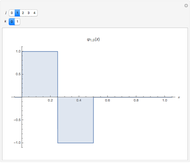
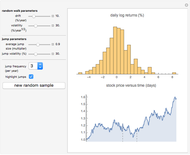
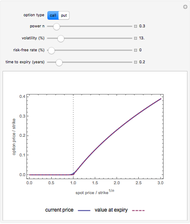
This Demonstration shows the Haar functions 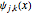, defined on the unit interval 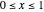for integers 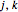, where 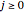and 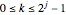. They form a complete orthogonal set on 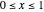and constitute the simplest type of wavelet.

Contributed by: Peter Falloon (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The Haar functions may be defined with respect to the "mother wavelet" 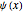, defined by

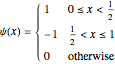
For integers and 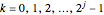, the Haar functions are then defined as .

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send