Chi-Squared Distribution and the Central Limit Theorem
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
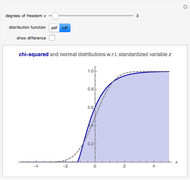
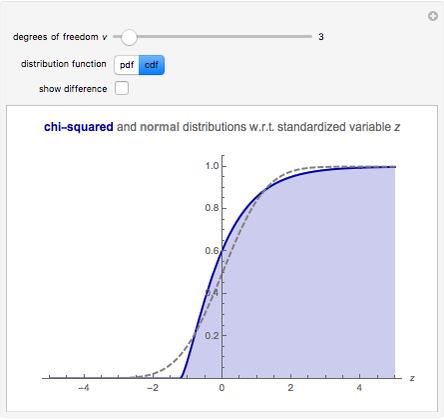
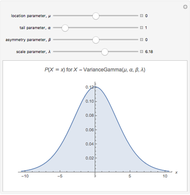
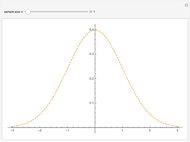
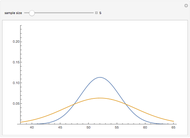
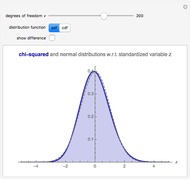
This Demonstration explores the chi-squared distribution for large degrees of freedom 
, which, when suitably standardized, approaches a standard normal distribution as 
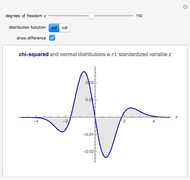
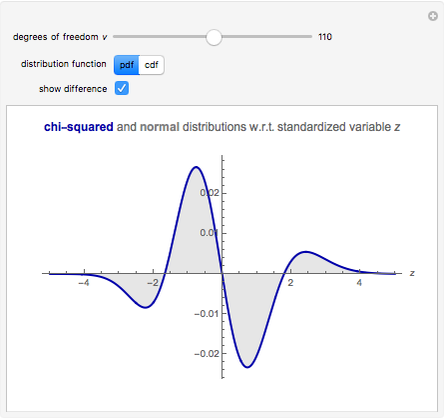
by the central limit theorem. In this Demonstration, can be varied between 1 and 2000 and either the PDF or CDF of the chi-squared and standard normal distribution can be viewed. You can also see the difference between the two distributions, which becomes useful for large .
Contributed by: Peter Falloon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
If 
are independent standard normal variables, then the random variable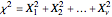 
follows the chi-squared distribution with mean and standard deviation 
. Taking the standardized variable 
, the central limit theorem implies that the distribution of 
tends to the standard normal distribution as .
It can be seen that the chi-squared distribution is skewed, with a longer tail to the right. However, the PDF has maximum value at 
(for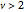 
), which is equivalent to 
, so the skew disappears in the limit as .
Permanent Citation
Variance-Gamma Distribution
Peter Falloon
Central Limit Theorem for the Continuous Uniform Distribution
David K. Watson
Central Limit Theorem Illustrated with Four Probability Distributions
D. Meliga and S. Z. Lavagnino
The Chi-Squared Distribution
Chris Boucher
Generalized Central Limit Theorem
Roger J. Brown and Bob Rimmer
The Central Limit Theorem
Chris Boucher
Illustrating the Central Limit Theorem with Sums of Uniform and Exponential Random Variables
Ian McLeod
Illustrating the Central Limit Theorem with Sums of Bernoulli Random Variables
Ian McLeod (University of Western Ontario)
Central Limit Theorem Applied to Samples of Different Sizes and Ranges
Mark D. Normand and Micha Peleg
Distribution of Normal Means with Different Sample Sizes
David Gurney
-
Option Prices in Merton's Jump Diffusion Model
Peter Falloon -
Chooser Options
Peter Falloon -
Binary Options: Pricing and Greeks
Peter Falloon -
Angular Spheroidal Functions as a Function of Spheroidicity
Peter Falloon -
Hyperbolic Distribution
Peter Falloon -
Variance-Gamma Distribution
Peter Falloon -
Options Board Using Black-Scholes Prices
Peter Falloon -
Properties of a Simple Random Walk with Boundaries
Peter Falloon -
Visualizing Superellipses
Peter Falloon -
Haar Functions
Peter Falloon -
Barrier Option Pricing within the Black-Scholes Model
Peter Falloon -
Clebsch-Gordan Coefficients
Peter Falloon -
Constant Coordinate Curves for Elliptic Coordinates
Peter Falloon -
Chi-Squared Distribution and the Central Limit Theorem
Peter Falloon -
Multiple Slit Diffraction Pattern
Peter Falloon -
Constant Coordinate Curves for Parabolic and Polar Coordinates
Peter Falloon -
Distribution of Returns from Merton's Jump Diffusion Model
Peter Falloon -
Pricing Power Options in the Black-Scholes Model
Peter Falloon -
Implied Volatility in Merton's Jump Diffusion Model
Peter Falloon -
Game Clock
Peter Falloon