Constant Coordinate Curves for Elliptic Coordinates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
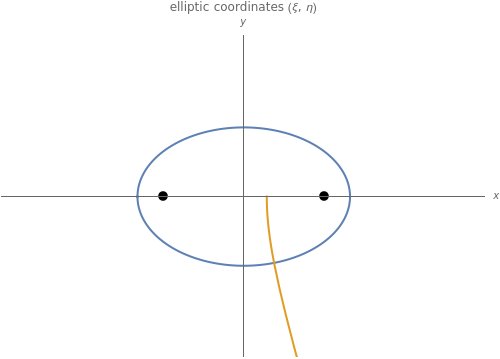
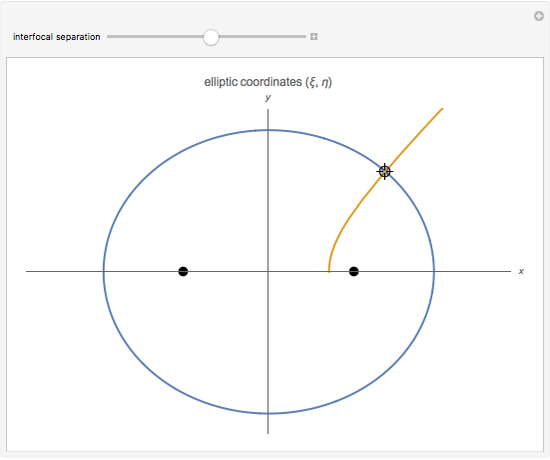
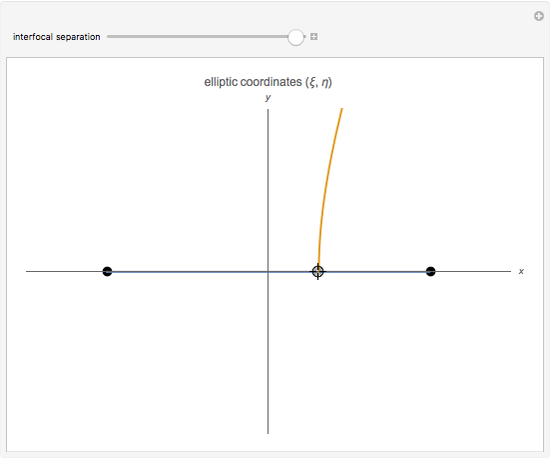
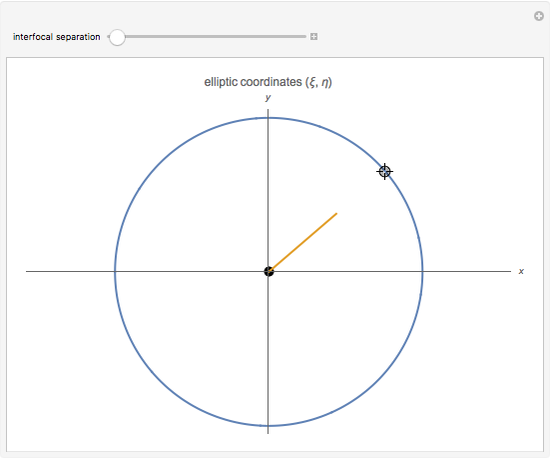
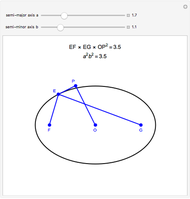
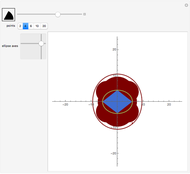
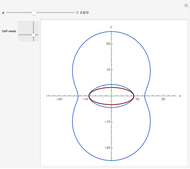
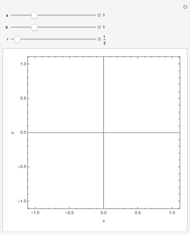
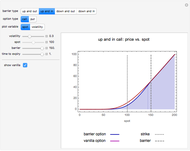
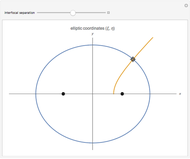
This Demonstration shows curves of constant coordinate values for the elliptic coordinate system in two dimensions. These curves are semi-hyperbolas and ellipses, the latter having foci at 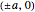 . As you drag the locator in the
. As you drag the locator in the 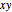 plane, the curves are redrawn so they pass through that point. Holding the mouse over the curve shows which variable is constant along that curve, and holding it over the point gives the actual values of the variables. You can vary the interfocal separation,
plane, the curves are redrawn so they pass through that point. Holding the mouse over the curve shows which variable is constant along that curve, and holding it over the point gives the actual values of the variables. You can vary the interfocal separation, 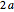 ; at
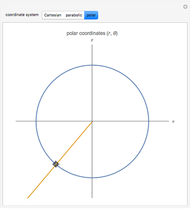
; at  the elliptic coordinates are equivalent to polar coordinates.
the elliptic coordinates are equivalent to polar coordinates.
Contributed by: Peter Falloon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Two-dimensional elliptic coordinates  may be defined by
may be defined by 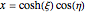 ,
, 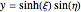 , for
, for 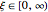 and
and 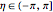 . The curves of constant
. The curves of constant  and
and  are ellipses and hyperbolas, respectively.
are ellipses and hyperbolas, respectively.
The inverse relation can be expressed 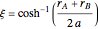 ,
, 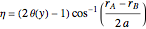 , where
, where 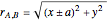 is the distance from the left/right focus. The slightly ungainly factor
is the distance from the left/right focus. The slightly ungainly factor  is necessary here to ensure that the correct (upper/lower) half-plane is chosen.
is necessary here to ensure that the correct (upper/lower) half-plane is chosen.
In the limit 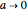 , the elliptic coordinates reduce to polar coordinates
, the elliptic coordinates reduce to polar coordinates 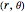 . The correspondence is given by
. The correspondence is given by 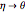 and
and  (note that
(note that  itself becomes infinite as
itself becomes infinite as 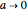 ).
).
Three-dimensional generalizations of the elliptic coordinates are the oblate and prolate spheroidal coordinates, elliptic cylindrical coordinates, and ellipsoidal coordinates.
Permanent Citation