Implied Volatility in Merton's Jump Diffusion Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
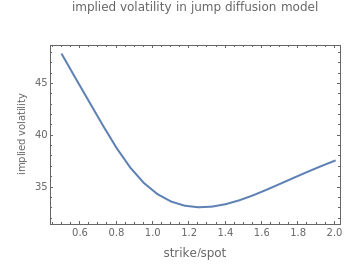
The "implied volatility" corresponding to an option price is the value of the volatility parameter for which the Black-Scholes model gives the same price. A well-known phenomenon in market option prices is the "volatility smile", in which the implied volatility increases for strike values away from the spot price. The jump diffusion model is a generalization of Black–Scholes in which the stock price has randomly occurring jumps in addition to the random walk behavior. One of the interesting properties of this model is that it displays the volatility smile effect. In this Demonstration, we explore the Black–Scholes implied volatility of option prices (equal for both put and call options) in the jump diffusion model. The implied volatility is modeled as a function of the ratio of option strike price to spot price.
Contributed by: Peter Falloon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the jump diffusion model, the stock price 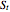 follows the random process
follows the random process 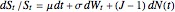 , which comprises, in order, drift, diffusive, and jump components. The jumps occur according to a Poisson distribution and their size follows a log-normal distribution. The model is characterized by the diffusive volatility
, which comprises, in order, drift, diffusive, and jump components. The jumps occur according to a Poisson distribution and their size follows a log-normal distribution. The model is characterized by the diffusive volatility  , the average jump size
, the average jump size 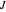 (expressed as a fraction of
(expressed as a fraction of 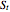 ), the frequency of jumps
), the frequency of jumps  , and the volatility of jump size
, and the volatility of jump size  .
.
In this Demonstration, you can vary the model parameters, along with the time to option expiry and the (constant) interest rate.
Note that, in addition to varying with the model parameters and strike/spot price ratio, the implied volatility is generally larger than the model diffusive volatility  ; this is essentially the extra volatility introduced by the jumps.
; this is essentially the extra volatility introduced by the jumps.
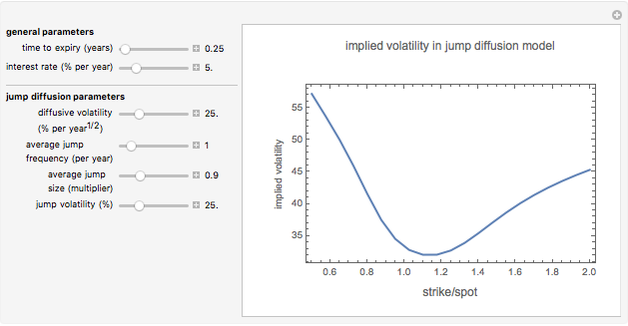
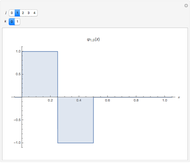
Snapshot 1: volatility smile in a jump diffusion model with downward jumps (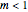 )
)
Snapshot 2: volatility smile with symmetric jumps (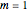 )
)
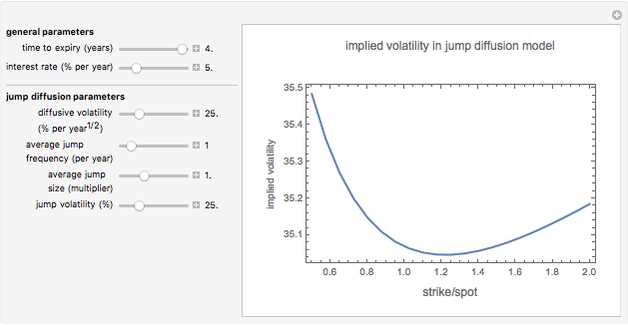
Snapshot 3: for long-dated options (here, time to expiry is four years) the smile is less pronounced
References:
R. Merton, Continuous‐Time Finance, Oxford: Blackwell, 1998.
M. Joshi, The Concepts and Practice of Mathematical Finance, Cambridge: Cambridge University Press, 2003.
Permanent Citation