Distribution of Returns from Merton's Jump Diffusion Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
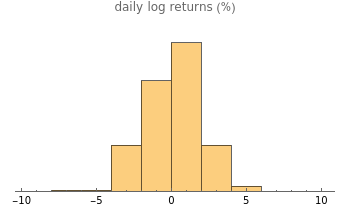
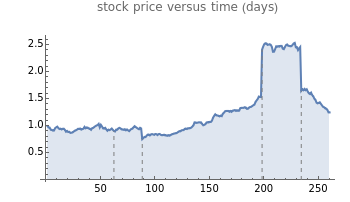
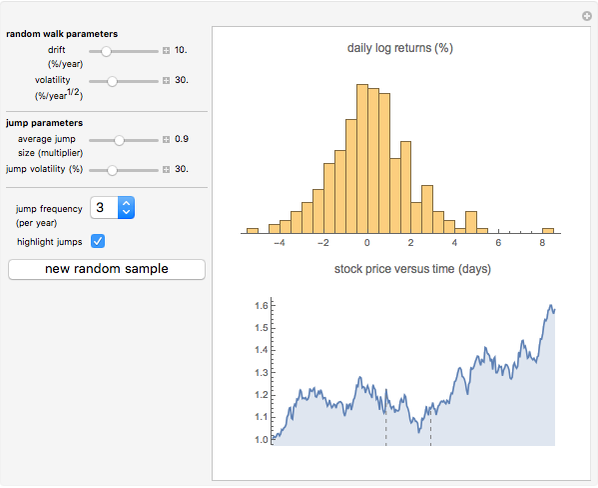
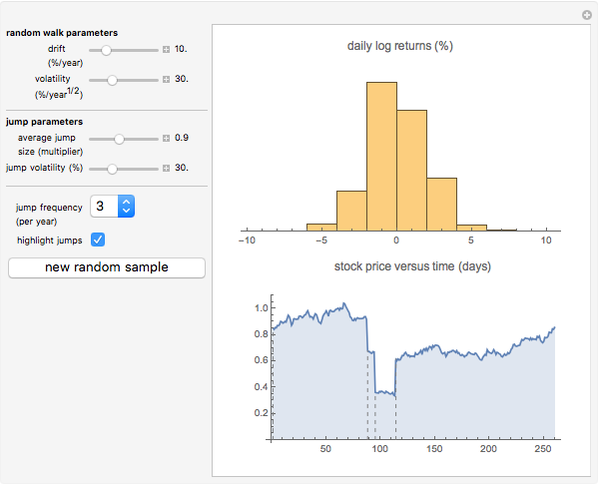
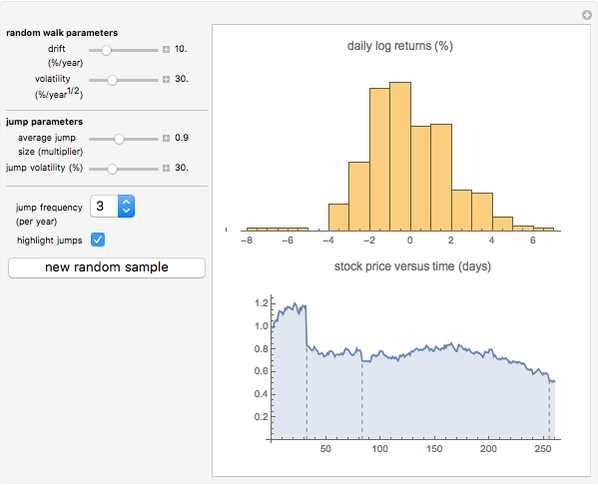
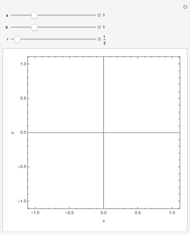
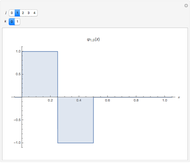
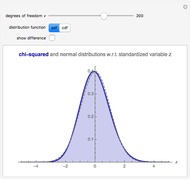
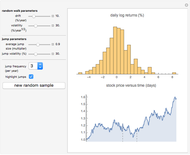
This Demonstration illustrates sample paths for an asset following Merton's jump diffusion model: the upper graph is a histogram of daily price returns, while the lower graph is the time series of price, both for a sample path of one year. The key feature of this model is that it incorporates large jumps; these show up as outliers in the histogram. The model parameters (namely, drift and volatility of the diffusive component, together with average size and volatility of the jumps) can be varied for a given sample. New random samples can be drawn, and the jump frequency (i.e., average number of jumps per sample) can be varied.
Contributed by: Peter Falloon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the jump diffusion model, the stock price 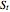 follows the random process
follows the random process  . The first two terms are familiar from the Black–Scholes model: drift rate
. The first two terms are familiar from the Black–Scholes model: drift rate  , volatility
, volatility  , and random walk (Wiener process)
, and random walk (Wiener process) 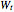 . The last term represents the jumps:
. The last term represents the jumps: 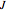 is the jump size as a multiple of stock price, while
is the jump size as a multiple of stock price, while 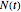 is the number of jump events that have occurred up to time
is the number of jump events that have occurred up to time  .
. 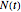 is assumed to follow the Poisson process
is assumed to follow the Poisson process 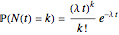 , where
, where 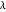 is the average frequency with which jumps occur. The jump size follows a log-normal distribution
is the average frequency with which jumps occur. The jump size follows a log-normal distribution 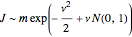 , where
, where 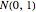 is the standard normal distribution,
is the standard normal distribution, 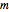 is the average jump size, and
is the average jump size, and  is the volatility of jump size.
is the volatility of jump size.
Snapshot 1: when there are no jumps, the jump diffusion model reduces to the Black–Scholes model, in which returns follow a normal distribution
Snapshot 2: the effect of jumps can be observed clearly by "turning down" the volatility of the diffusive component to zero
Snapshot 3: one limitation of the jump diffusion model is that is the volatility in the diffusive component is constant, which results in unrealistic-looking behavior when the jumps are large: in reality, volatility tends to increase dramatically around the time that large jumps occur.
References:
R. Merton, Continuous-Time Finance, Cambridge, MA: B. Blackwell, 1998.
M. Joshi, The Concepts and Practice of Mathematical Finance, New York: Cambridge University Press, 2003.
Permanent Citation
"Distribution of Returns from Merton's Jump Diffusion Model"
http://demonstrations.wolfram.com/DistributionOfReturnsFromMertonsJumpDiffusionModel/
Wolfram Demonstrations Project
Published: March 7 2011