Hysteresis in the Flow Curves of Pseudoplastic Semiliquid Foods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
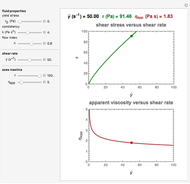
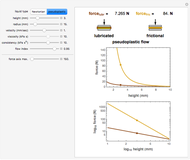
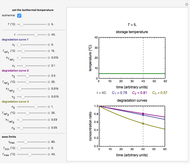
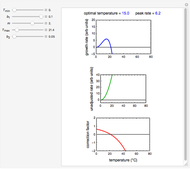
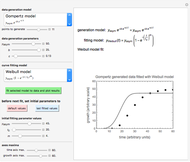
Shearing a pseudoplastic semiliquid food, such as fruit juice concentrate or nectar, in a viscometer frequently disrupts its microstructure. Consequently, the flow curve recorded by first raising and then lowering the shear rate exhibits a hysteresis loop. The loop's area represents the energy dissipated in the shearing process in terms of power per unit volume. This Demonstration shows the phenomenon in simulated flow curves accompanied by the calculated hysteresis area.
Contributed by: Mark D. Normand and Micha Peleg (July 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
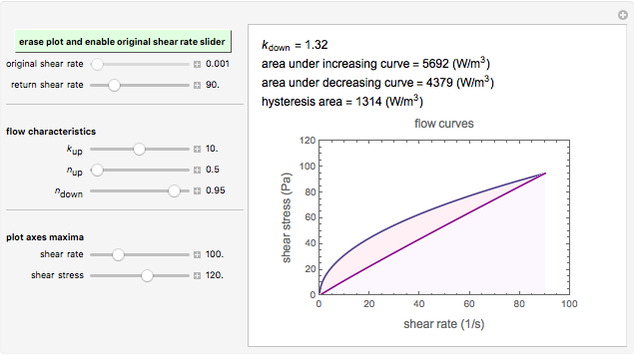
Snapshot 1: strongly pseudoplastic fluid, showing large hysteresis
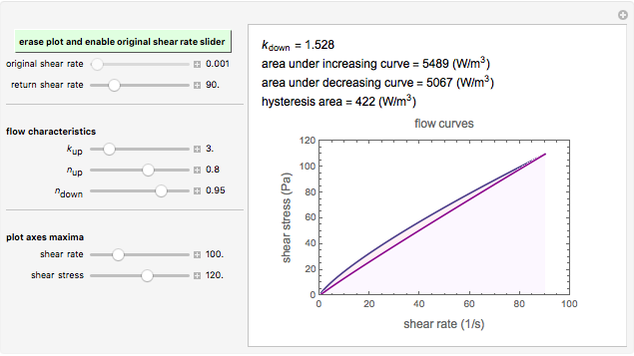
Snapshot 2: weakly pseudoplastic fluid, showing small hysteresis
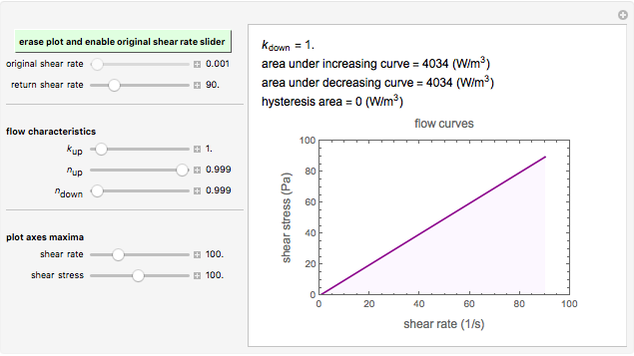
Snapshot 3: almost perfectly Newtonian fluid, showing no hysteresis
The flow curve of a pseudoplastic ("shear thinning," "power-law") fluid is described by the equation 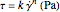 , where
, where  is the shear stress,
is the shear stress,  is the shear rate in
is the shear rate in 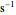 ,
,  is the "consistency" in the corresponding units, and
is the "consistency" in the corresponding units, and  is the "flow index" (dimensionless). Thus, the curve for the increasing shear rate is
is the "flow index" (dimensionless). Thus, the curve for the increasing shear rate is 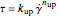 , and for the decreasing rate it is
, and for the decreasing rate it is 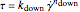 , where
, where  and
and 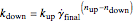 ;
; 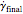 is the shear rate turnover point. (Theoretically, the flow index
is the shear rate turnover point. (Theoretically, the flow index  can vary between zero and one. In practice, however, if an experimentally determined value is found to be much smaller than about 0.5, one should suspect slip in the rheometer's sensor.)
can vary between zero and one. In practice, however, if an experimentally determined value is found to be much smaller than about 0.5, one should suspect slip in the rheometer's sensor.)
The area under a shear stress versus shear rate curve has the dimension of power per unit volume. For the increasing shear rate mode, it is 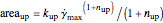 , and for the decreasing shear rate,
, and for the decreasing shear rate, 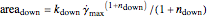 . The hysteresis loop area is therefore
. The hysteresis loop area is therefore 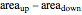 .
.
In this Demonstration, the pair of flow curves, up (increasing) and down (decreasing), is generated by dragging the original shear rate slider from its minimum value to its maximum and back to its minimum. To erase an existing plot and enable the grayed-out original shear rate slider, click the "erase plot and enable original shear rate slider" setter. After the existing flow curves are erased, move the original shear rate slider from its minimum to maximum to minimum values again. The upper limit of the original shear rate slider and the curves on the plot are set by the return shear rate slider. The "erase plot and enable original shear rate slider" setter only becomes active (colored light green) after the original shear rate slider has been moved through a complete minimum to maximum to minimum cycle, at which time the original shear rate slider becomes grayed out and inactive. The magnitudes of 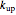 ,
, 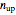 , and
, and  , as well as the plot's axes maxima, are chosen with sliders. The display includes a plot of the two flow curves (up and down), with the hysteresis loop area highlighted in a different color. The display also lists the numerical values of the calculated
, as well as the plot's axes maxima, are chosen with sliders. The display includes a plot of the two flow curves (up and down), with the hysteresis loop area highlighted in a different color. The display also lists the numerical values of the calculated  , the areas under each of the two flow curves and that of the hysteresis loop in
, the areas under each of the two flow curves and that of the hysteresis loop in 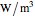 after a complete minimum to maximum to minimum cycle of the original shear rate slider has been completed and the "erase plot and enable original shear rate slider" setter has become active.
after a complete minimum to maximum to minimum cycle of the original shear rate slider has been completed and the "erase plot and enable original shear rate slider" setter has become active.
Permanent Citation