Structure of Dilute Suspensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
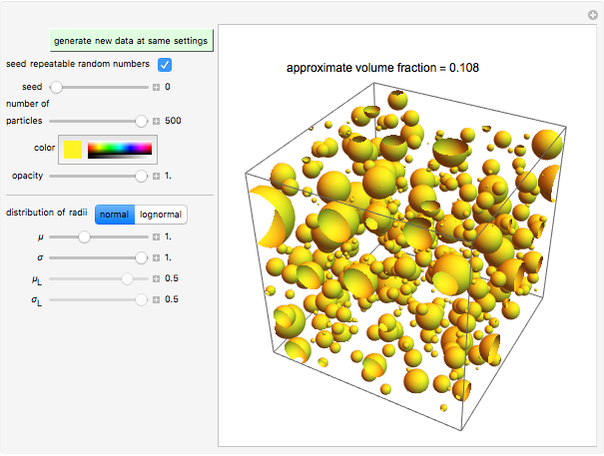
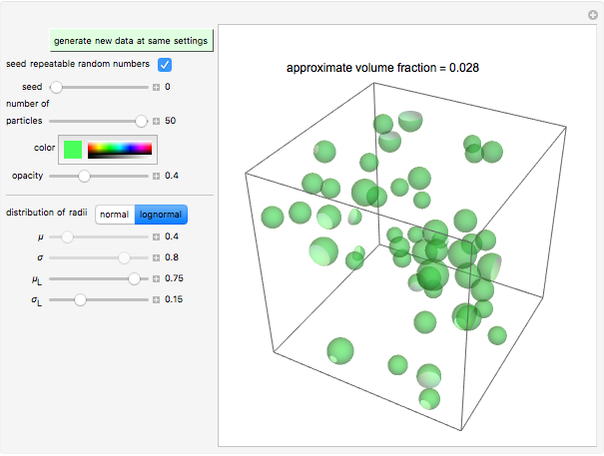
The visual appearance of randomly suspended particles in a given volume is determined by their number, shape, size, and spatial distribution. This Demonstration simulates the 3D structures of random suspensions of spherical particles whose diameters follow a normal or lognormal distribution, and calculates their volume fraction. The simulated suspensions can then be viewed from different angles.
Contributed by: Mark D. Normand and Micha Peleg (February 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
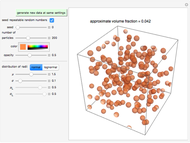
Snapshot 1: normally distributed spheres with a small standard deviation
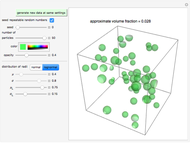
Snapshot 2: normally distributed spheres with a large standard deviation
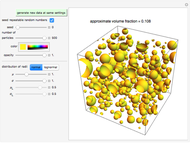
Snapshot 3: lognormally distributed spheres with a small standard deviation
Snapshot 4: lognormally distributed spheres with a large standard deviation
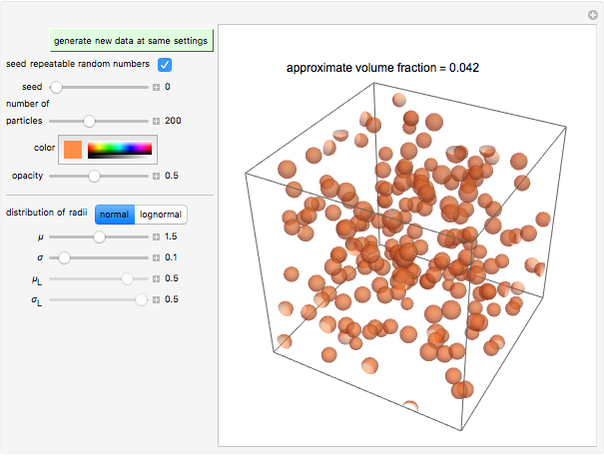
This Demonstration simulates the appearance of randomly suspended spherical particles. You can vary the number of spheres and the spatial distribution of their centers by the corresponding sliders, "seed" and "number of particles". You can also select their color and opacity with sliders. You can choose the sphere radii's size distribution (normal or lognormal with a setter bar) and the corresponding mean and standard deviation (or logarithmic mean and standard deviation) in arbitrary units, using the sliders.
The program plots the spheres inside a cubic box of fixed size and calculates their volume fraction, which is displayed above the image. To view the particles from different angles, rotate the image by dragging it.
Permanent Citation
"Structure of Dilute Suspensions"
http://demonstrations.wolfram.com/StructureOfDiluteSuspensions/
Wolfram Demonstrations Project
Published: February 26 2014