Mathematica MathWorld Wolfram Science More »

Investment Returns


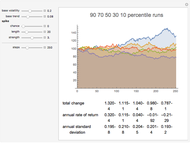
	Investment returns from regular savings with random performance.


	Contributed by: Jason Cawley

The average ending value is of the random sample used, not an overall expected value.

Returns are expected to be distributed log-normally around the expected return.

Withdrawal questions can be addressed by using a negative annual investment.

The increase amount per year parameter can track savings rising with income, or cost-of-living adjustments on withdrawals.

All parameters should be annualized figures.

Period should be the frequency of new savings or withdrawals.

Adjusting the sample size to a new figure and back will generate a new set of random returns.

Test proposed withdrawal rates for a low chance of depleting capital by watching the lowest series in a large sample.

The savings rate and time do most of the work. Increase either to reach a set goal.

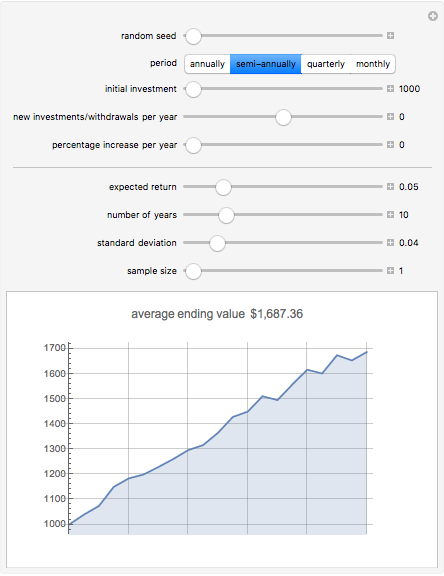
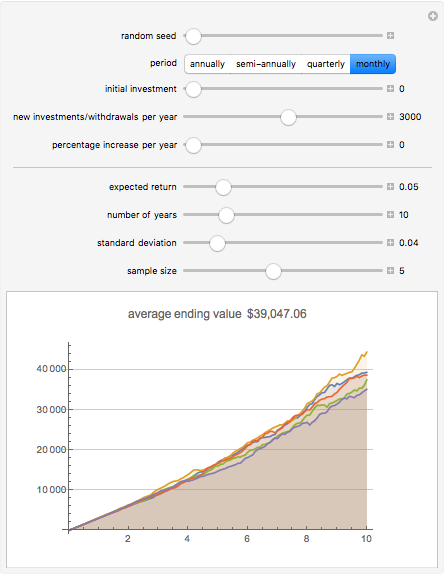
Typical expected returns for cash equivalents can be set to 5%, or the prevailing short-term interest rate.

Typical expected returns for bonds can be set at 6 to 7%, or at the prevailing interest rate on long-term corporates.

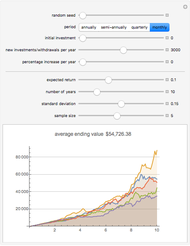
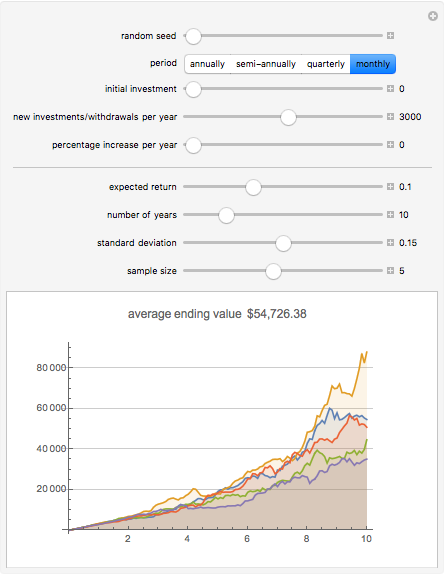
Typical expected returns for stocks can be set to 10%, or at dividend yield plus nominal economic growth.

Typical standard deviation for cash equivalents can be set to 0, or 1 to 2% for short-term bonds.

Typical standard deviation for bonds can be set to 4 to 5%, or the approximate bond portfolio duration.

Typical standard deviation for stocks can be set to 15%, or 20% for riskier asset classes.

Snapshot 1: Typical return of a one-time bond fund investment over 10 years.

Snapshot 2: Regular savings of $3000 per year invested in a bond fund; 5% expected with 4% standard deviation.

Snapshot 3: The same savings into a stock fund with 10% expected, but 15% standard deviation.

Snapshot 4: 20 years of savings in a balanced portfolio, 8% expected and 10% standard deviation.

Snapshot 5: 20 year balanced with 3% annual increases in the amount saved and a $5000 initial investment.

Snapshot 6: Regular withdrawals equal to the expected return frequently result in a large fall in capital.

Snapshot 7: Taking less than the full expected return lowers risk and can readily handle a long series of rising payouts.

Contributed by: Jason Cawley

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom