Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Mixing in Two Connected Tanks

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Contributed by: Stephen Wilkerson (March 2011)
(United States Military Academy West Point, Department of Mathematics)
Open content licensed under CC BY-NC-SA

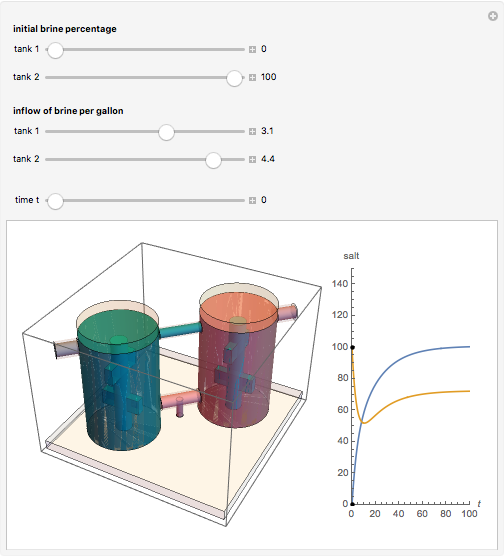
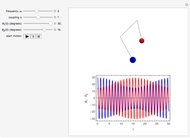
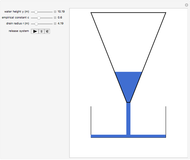
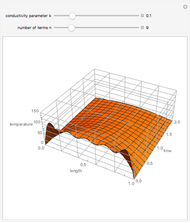
Snapshots

Details

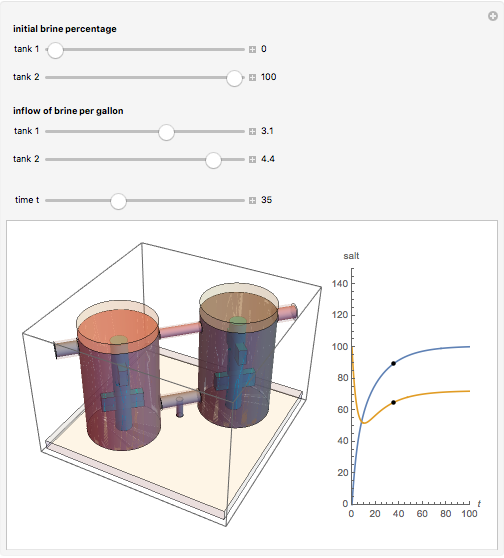
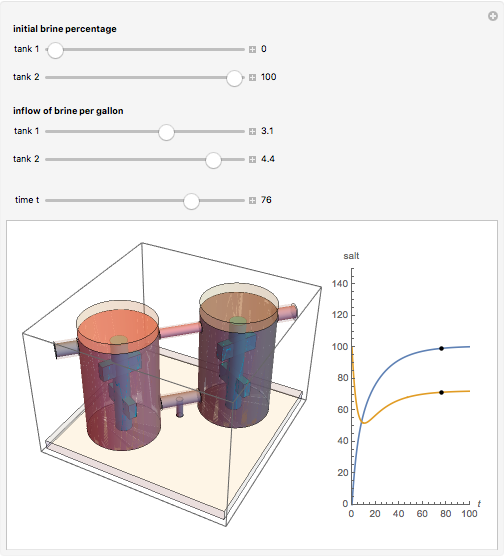
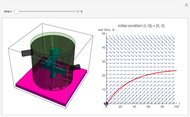
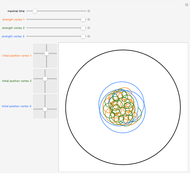
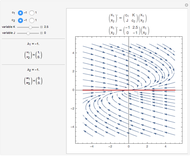
This example comes from [1], Section 3.2, Fluid Flow in Tanks, following problem 30.

Reference

[1] J. R. Brannan and W. E. Boyce, Differential Equations with Boundary Value Problems: An Introduction to Modern Methods and Applications, New York: John Wiley and Sons, 2010.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send