Modified Logistic Isothermal Microbial Growth Ratio

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
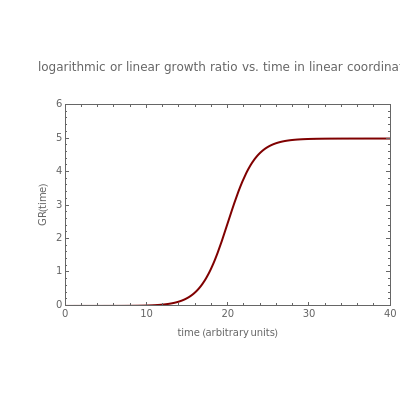
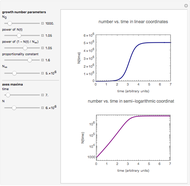
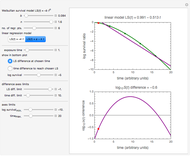
This Demonstration contains a plot that simulates the rise of a microbial population's growth ratio, 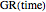 , in a food at constant temperature. You can modify the growth ratio curve by slider-controlled settings of three growth ratio parameters of a modified logistic function.
, in a food at constant temperature. You can modify the growth ratio curve by slider-controlled settings of three growth ratio parameters of a modified logistic function.
Contributed by: Mark D. Normand and Micha Peleg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
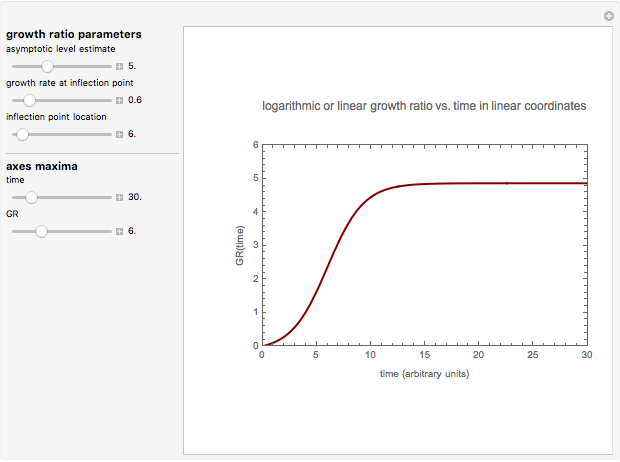
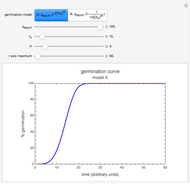
Snapshot 1: growth curve with a very short lag time expressed as a ratio vs. time
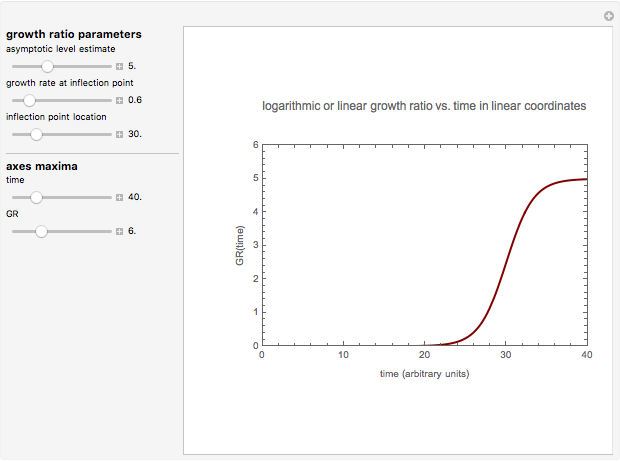
Snapshot 2: growth curve with a long lag time expressed as a ratio vs. time
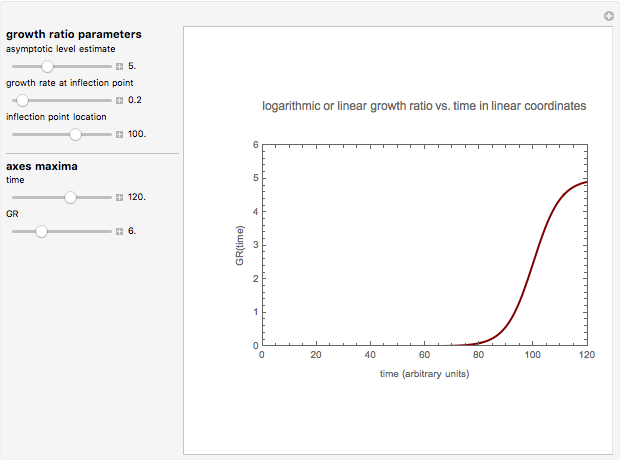
Snapshot 3: growth curve with an extremely long lag time expressed as a ratio vs. time
This Demonstration contains a plot of the rise in the growth ratio produced by a modified version of the logistic function formulated as 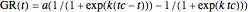 . The growth ratio itself,
. The growth ratio itself, 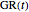 , can be defined either as logarithmic, that is,
, can be defined either as logarithmic, that is, 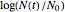 (base 10 or natural log) or linear, that is,
(base 10 or natural log) or linear, that is, 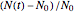 , where
, where 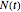 is the actual number (count) and
is the actual number (count) and  is the initial number of cells. In either case, at
is the initial number of cells. In either case, at  , the ratio is also zero.
, the ratio is also zero.
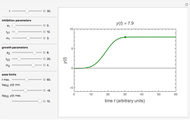
The Demonstration can be used to model isothermal microbial growth in foods by slider-controlled manipulation of three growth parameters: an estimate of the asymptotic growth ratio,  , the normalized rate at the curve's inflection point,
, the normalized rate at the curve's inflection point,  , and the inflection point's location,
, and the inflection point's location, 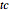 . Two other sliders control the maximum settings of the time and growth ratio axes. The model is particularly suitable for generating growth curves with a long (logarithmic) lag time for which the conventional Verhulst model is inappropriate. The generated plot is very similar to that produced by the Gompertz model. The difference, apart from its mathematical structure, is that each of the parameters has an intuitive meaning and can be varied independently.
. Two other sliders control the maximum settings of the time and growth ratio axes. The model is particularly suitable for generating growth curves with a long (logarithmic) lag time for which the conventional Verhulst model is inappropriate. The generated plot is very similar to that produced by the Gompertz model. The difference, apart from its mathematical structure, is that each of the parameters has an intuitive meaning and can be varied independently.
Although the model was originally developed to describe microbial growth patterns, the program can also be used to model growth phenomena in other areas such as economics.
Please note that not all possible parameter combinations necessarily yield a realistic growth curve.
For more on the model and its application in foods see: M. G. Corradini and M. Peleg, "Estimating non-isothermal bacterial growth in foods from isothermal experimental data," Journal of Applied Microbiology, 99, 2005 pp. 187-200, and M. Peleg, "Advanced quantitative microbiology for food and biosystems: Models for predicting growth and inactivation," 2006 CRC Press, Boca Raton FL.
Permanent Citation